Question

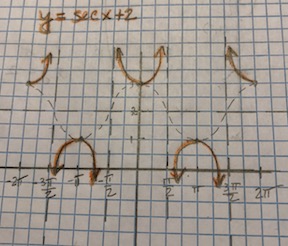
How do you graph `y=secx+2`?

Answer 1

See answer below

Explanation:

Given: `y = sec x + 2`

First draw a dashed vertical shift line at `y = 2`

Since `sec x = 1/(cos x)`, sketch a dashed cosine function

`y = cos x + 2 => " amplitude" = 1 " and period " = 2 pi`

Remember that a cosine with a period of `2 pi` needs to be divided into 4 sections: `0, pi/2, pi, (3pi)/2, 2 pi`.

Wherever the cosine function crosses the `y = 2` line there will be a vertical asymptote. At each peak and trough, there will be a point on the secant function that arcs up to the adjacent vertical asymptotes: