Question

How do you graph `y= |x+1|`?

Answer 1

graph{y=|x+1| [-8.08, 7.68, -1.54, 6.336]}
Shift `y=|x|`
or
Sketch two linear functions (lines)

Explanation:

The easiest way to do this is to just shift the graph of `y=|x|` one unit to the left.

We can see this a lot more clearly if we set `f(x) = |x|`, so `f(x+1)=|x+1|`, indicating a one unit shift to the left.

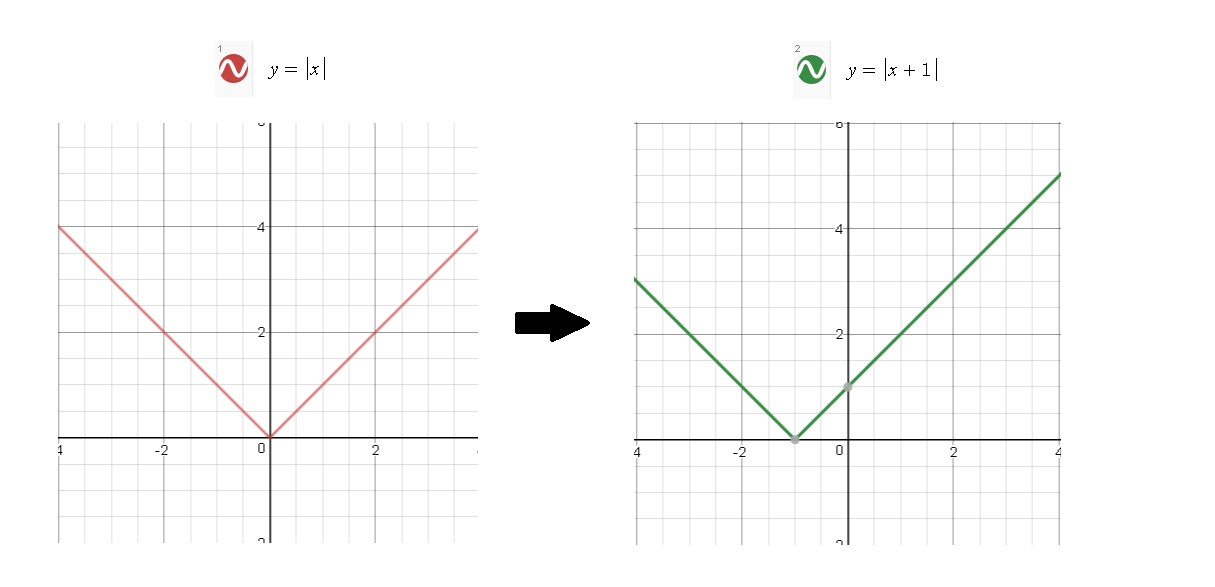
An alternative way of graphing `y=|x+1|` is to think of it as two linear functions. The function depends on whether `x+1` is negative or positive.

We know when `x >= -1`, `y = x+1`

and when `x < -1`, `y = -x-1`

We can rewrite this as a piecewise function:

`f(x) = { (x>= -1 ", " x+1), (x<-1 ", " -x-1) :}`

We essentially sketch the graph of `y=x+1` on the right of `x=-1`

and we sketch the graph of `y=-x-1` on the left of `x=-1`.