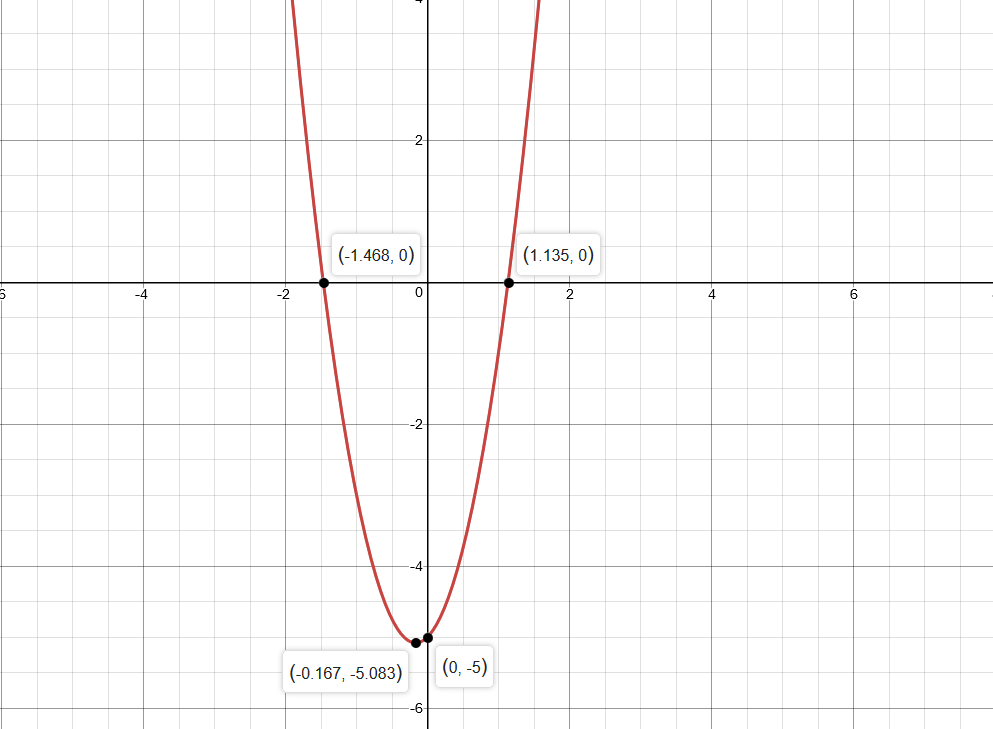
How do you identify the important parts of #f(x)= 3x²+x-5# to graph it?
1 Answer
Jul 24, 2018
Vertex
y-intercept
X-intercepts
Explanation:
Given -
#f(x)=3x^2+x-5#
#y=3x^2+x-5#
Vertex
#x=(-b)/(2a)=(-1)/(2xx3)=-1/6#
At
#y=1/12-1/6-5=(1-2-60)/12=61/12=-61/4#
Vertex
y-intercept
At
y-intercept#(0,-5)
x-intercepts
#3x^2+x=5#
#x^2+1/3x=5/3#
#x^2+1/3x+1/36=5/3+1/36=(60+1)/36=61/36#
#(x+1/6)^2=61/36#
#x+1/6=+-sqrt(61/36)=+-sqrt61/6#
#x=sqrt(61/6)-1/6=(sqrt61-1)/6#
#x=-sqrt(61/36)-1/6=-(sqrt61-1)/6#
X-intercepts