Question

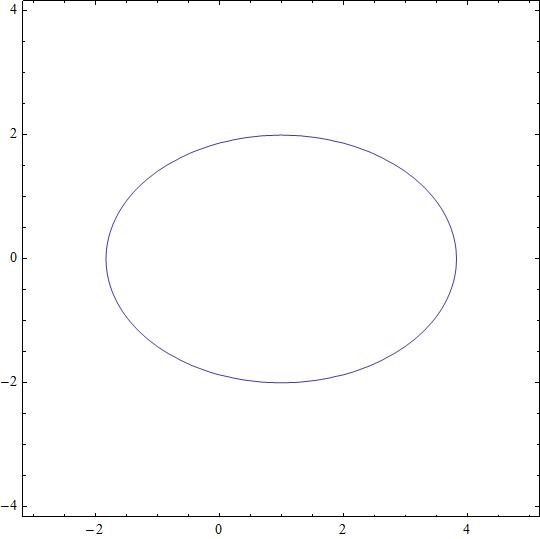
How do you identify the type of conic `4x^2+8y^2-8x-24=4` is, if any and if the equation does represent a conic, state its vertex or center?

Answer 1

An ellipse

Explanation:

Conics can be represented as

`p cdot M cdot p+<< p, {a,b}>>+c=0`

where `p = {x,y}` and

`M = ((m_{11},m_{12}),(m_{21}, m_{22}))`.

For conics `m_{12} = m_{21}` then `M` eigenvalues are always real because the matrix is symetric.

The characteristic polynomial is

`p(lambda)=lambda^2-(m_{11}+m_{22})lambda+det(M)`

Depending on their roots, the conic can be classified as

1) Equal --- circle
2) Same sign and different absolute values --- ellipse
3) Signs different --- hyperbola
4) One null root --- parabola

In the present case we have

`M = ((4,0),(0,8))`

with characteristic polynomial

`lambda^2-12lambda+32=0`

with roots `{4,8}` so we have an ellipse.

Being an ellipse there is a canonical representation for it

`((x-x_0)/a)^2+((y-y_0)/b)^2=1`

`x_0,y_0,a,b` can be determined as follows

`4 x^2 + 8 y^2 - 8 x - 28-(b^2(x-x_0)^2+a^2(y-y_0)^2-a^2b^2)=0 forall x in RR`

giving

#{ (-28 + a^2 b^2 - b^2 x_0^2 - a^2 y_0^2 = 0), (2 a^2 y_0 = 0), (8 - a^2 = 0), (-8 + 2 b^2 x_0 = 0), (4 - b^2 = 0) :}#

solving we get

`{a^2 = 8, b^2 = 4, x_0 = 1, y_0 = 0}`

so

`{4 x^2 + 8 y^2 - 8 x - 24=4}equiv{(x-1)^2/8+y^2/4=1}`