Question

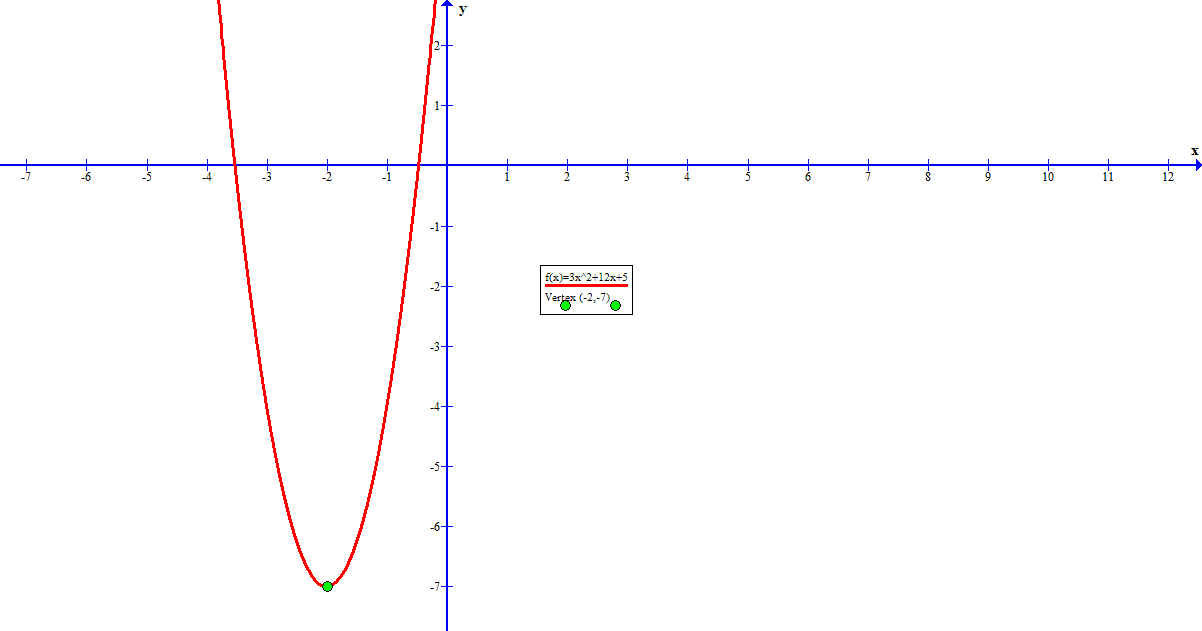
How do you Identify the vertex for the graph of `y = 3x^2 + 12x + 5`?

Answer 1

The easiest way is to convert the given equation into vertex form to determine that the vertex is at `(-2,-7)`

Explanation:

The vertex form is
`color(white)("XXX")y=color(green)m(x-color(red)a)^2+color(blue)b`
with vertex at `(color(red)a,color(blue)b)`

Given `y=3x^2+12x+5`

Extract the `color(green)m` factor from the first 2 terms:
`color(white)("XXX")color(green)3(x^2+4x)+5`

Complete the square
`color(white)("XXX")y=color(green)3(x^2+4xcolor(magenta)(+2^2))+5color(magenta)(-color(green)3 * (2^2))`

Simplify into vertex form:
`color(white)("XXX")y=color(green)3(x+2)^2-7`
or
`color(white)("XXX")y=color(green)3(x-color(red)(""(-2)))^2+color(blue)(""(-7))`
with vertex at `(color(red)(-2),color(blue)(-7))`

and because I like pictures to verify my work, here is a graph of the original equation plus the determined vertex point: