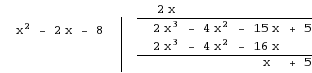First divide the numerator by the denominator using long division.
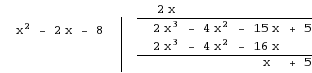
So, our new integral is #int(2x + (x + 5)/(x^2 - 2x - 8))dx#
We now can write #(x + 5)/(x^2 - 2x - 8)# in partial fractions.
First of all, #x^2 - 2x - 8# can be factored as #(x- 4)(x + 2)#.
#A/(x- 4) + B/(x + 2) = (x + 5)/((x- 4)(x + 2))#
#A(x + 2) + B(x- 4) = x + 5#
#Ax + 2A + Bx - 4B = x + 5#
#(A + B)x + (2A - 4B) = x + 5#
We can now write a system of equations.
#{(A + B = 1), (2A - 4B = 5):}#
Solving:
#B = 1 - A#
#2A - 4(1 - A) = 5#
#2A - 4 + 4A = 5#
#6A = 9#
#A = 3/2#
#B = -1/2#
Hence, the partial fraction decomposition of #(x + 5)/(x^2- 2x - 8)# is #3/(2(x - 4)) - 1/(2(x + 2))#
The integral now becomes:
#int(2x + 3/(2(x - 4)) - 1/(2(x + 2)))dx#
Which can be readily integrated as;
#x^2 + 3/2ln|x - 4| - 1/2ln|x + 2| + C# using the rule #int(1/u)du = ln|u| + C# and #int(x^n)dx = (x^(n + 1))/(n + 1)#. You can check the result by differentiating.
Hopefully this helps!