Question

How do you know what trigonometric function to use to solve right triangles?

Answer 1

Right triangles are a special case of triangles. You always know at least one angle, the right angle, and depending on what else you know, you can solve the rest of the triangle with fairly simple formulas.

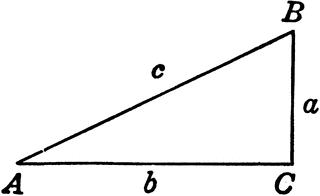
If you know any one side and one angle, or any two sides, you can use the pneumonic soh-cah-toa to remember which trig function to use to solve for others.

`ul s i n( theta) =` `ul o`pposite`/` `ul h`ypotenuse
`ul c os(theta) = ul a`djacent`/ul h`ypotenuse
`ul t an(theta) = ul o`pposite`/ul a`djacent

Opposite refers to the side which is not part of the angle, adjacent refers to the side that is part of the angle, and the hypotenuse is the side opposite the right angle, which is `C` in the image above.

For example,lets say you know the length of `a` and the value of angle `A` in the above triangle. Using the cosine function you can solve for `c`, the hypotenuse.

`cos(A) = a / c`

Which rearranges to;

`c = a/cos(A)`

If you know the length of both sides `a` and `b`, you can solve for the tangent of either angle `A` or `B`.

`tan(A) = a/b`

Then you take the inverse tangent, `tan^-1` to find the value of `A`.