What will be the length of the shadow of the tower, correct to the nearest meter, on a day that the the angle of elevation of the sun is 50 deg given that the tallest freestanding structure in the world is the 553 meter high?

Question

3503 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-02-05T11:48:51

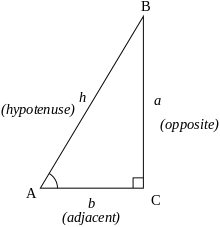
enter image source here

Let #a# be the tower (#553 m#) and #b# the shadow,
and #angleA# is the angle of elevation (#50^0#)

The tangent of #angleA# is defined as #a/b#

We fill in what we know:

#tanA=a/b->tan50^0=553/b->1.1918=553/b#

#->b=553/1.1918=464# meter