Question

How do you plot the Arrhenius equation?

Answer 1

You draw a graph of `lnk` vs. `1/T`.

Explanation:

The Arrhenius equation is

`k = Ae^(-E_a//RT)`

where

• `k` is the rate constant
• `A` is the pre-exponential factor
• `E_a` is the activation energy
• `R` is the universal gas constant
• `T` is the temperature

If we take the logarithms of both sides, we get

`lnk = lnA color(white)(l)–E_a/(RT)`

or

`lnk = -(E_a/R)1/T + lnA`

This is the equation of a straight line

`y = mx + b`

where `m` is the slope and `b` is the slope of a plot of `y` vs `x`.

`lnk = ("-"E_a/R)1/T + lnA`
`color(white)(ll)y =color(white)(mm) mcolor(white)(mll)xcolor(white)(ll) + color(white)(ll) b`

By comparing the equations, we see that the slope of the line is `"-"E_a/R` and the `y` intercept is `lnA`

Hence, if we draw a graph of `lnk` vs. `1//T` at various temperatures, we should get a straight line.

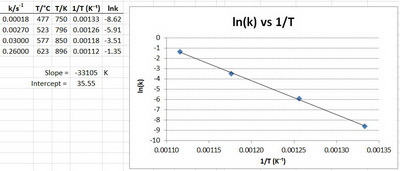
Example

For a certain reaction, the data were:

`bbTbb"/°C" color(white)(ml)bb"k/s"^"-1"`
`color(white)(ll)477 color(white)(mll) 0.00018`
`color(white)(ll)523color(white)(mll)0.0027`
`color(white)(ll)577color(white)(mll)0.030`
`color(white)(ll)623 color(white)(mll)0.26`

Plot the Arrhenius equation using the above values.

Solution

We have to plot `lnk` vs `1//T`.

We must convert the temperatures to kelvins and take their reciprocals.

We must also take the natural logarithms of the rate constants.

Although we could do this by hand, I find it easier to do the calculations and the plot in Excel.

Here's are my results.