Question

How do you prove Ptolemy's Theorem that in a cyclic quadrilateral, sum of the products of opposite pair of sides is equal to the product of the diagonals?

In cyclic quadrilateral `ABCD`, `ABxxCD+BCxxAD=ACxxBD`.

Answer 1

Please see below.

Explanation:

Let `ABCD` be the cyclic quadrilateral inscribed in a circle as decsribed below. Let us also join its diagonals `AC` and `BD` to intersect at `P`.

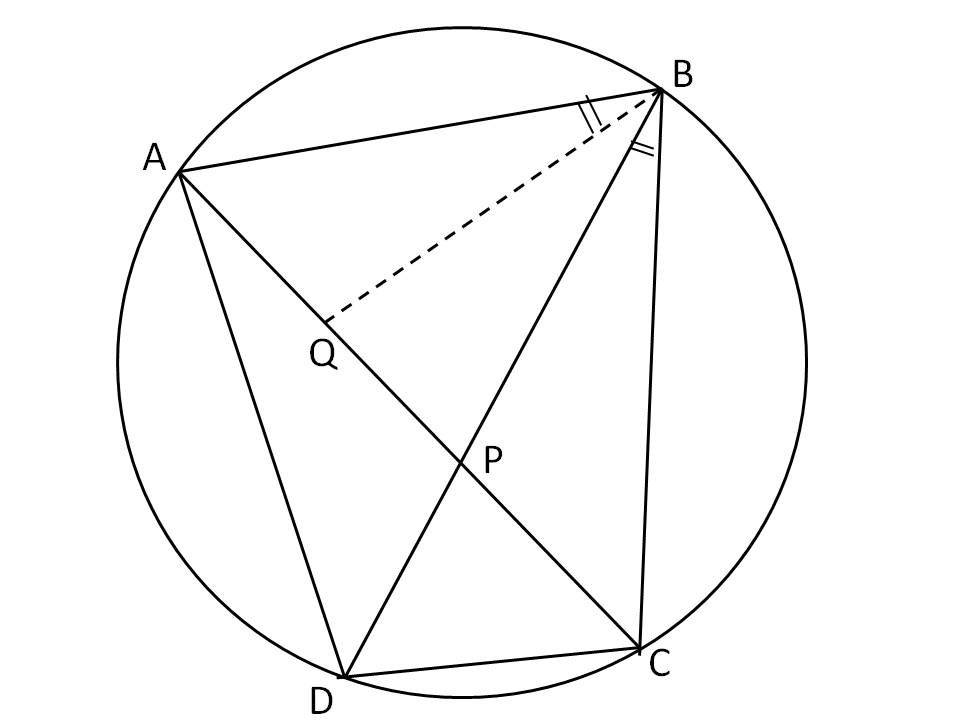
To prove that `ABxxCD+BCxxAD=ACxxBD`, let us draw an angle `/_ABQ=/_CBD` to intersect `AC` at `Q`, as shown.

Now in `DeltaABQ` and `DeltaCBD`, we have

`/_ABQ=/_CBD` - by construction
`/_BAQ=/_CDB` - angles in the same arc `BC`

`:.DeltaABQ~DeltaCBD`

and hence corresponding sides are proportional

`(AB)/(BD)=(AQ)/(CD)` or `ABxxCD=BDxxAQ` ..........(1)

Similarly as `/_ABQ=/_CBD`, we have `/_ABQ+/_QBP=/_CBD+/_QBP`

or `/_ABD=/_QBC` and in `DeltaABD` and `DeltaQBC`, we have

`/_ABD=/_QBC`
`/_ADB=/_QCB` - angles in the same arc `AB`

`:.DeltaABD~DeltaQBC`

and hence corresponding sides are proportional

`(AD)/(QC)=(BD)/(BC)` or `ADxxBC=BDxxQC` ..........(2)

Adding 1 and 2, we get

`ABxxCD+ADXXBC=BDxx(AQ+QC)=BDxxAC`