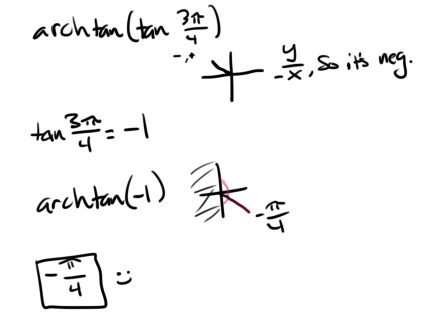
How do you simplify #arctan (tan 3pi/4)#?
1 Answer
Nov 5, 2015
Explanation:
To solve this you must first solve the inside. Now think about it...
Now that we have simplified it into
Here is the work written out if this helps you more.