Firstly, note that for the range of #arcsin(\frac{x}{5})#, the cosine function is purely positive.
Thus, I can say,
#cos(arcsin(\frac{x}{5})) = sqrt{1-sin^2(arcsin(\frac{x}{5}))}#, and also for the domain of x, #sin(arcsin(\frac{x}{5})) = \frac{x}{5}# since the arcsine function outputs values ranging from #-\frac{pi}{2}# to #\frac{pi}{2}#.
This can be verified graphically, the red one being #cos(arcsin(\frac{x}{5}))#, green #cos(\frac{x}{5})#, and blue #arcsin(\frac{x}{5})#: 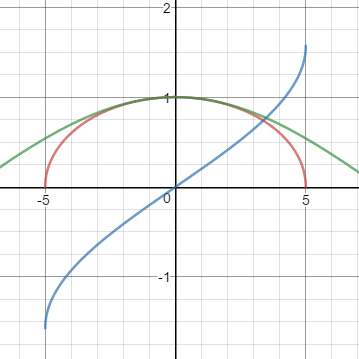
Therefore,
#cos(arcsin(\frac{x}{5})) = sqrt{1-\frac{x^2}{25})#
#= \frac{sqrt{25-x^2}}{5}#.
