Question

How do you simplify `(x + 5y)^3`?

Answer 1

There are two ways of approaching this problem.

Explanation:

a) Simple multiplication of binomials:

`(x + 5y)(x + 5y)(x + 5y)`

`=(x^2 + 10xy + 25y^2)(x + 5y)`

`=x^3 + 10x^2y + 25xy^2 + 5x^2y + 50xy^2 + 125y^3`

`=x^3 + 15x^2y + 75xy^2 + 125y^3`

b) Binomial theorem or Pascal's Triangle:

Here in British Columbia, we teach the binomial theorem and Pascal's Triangle in order to facilitate binomial expansions where in `(a + b)^n`, `n >= 3`, although you could do it for any value of n.

The method I will show you involves Pascal's Triangle since this is probably easiest for you to comprehend. The following image shows Pascal's Triangle.

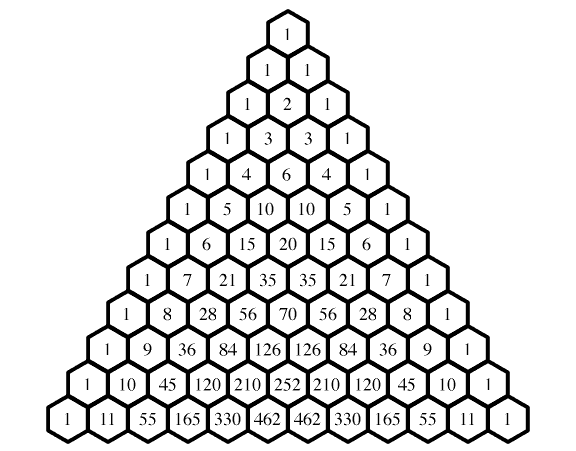
What do you notice?

You probably immediately notice that the sum of the number directly below two numbers is the sum of the two numbers above it (for example, 1 and 1 are directly above 2, since `1 + 1 = 2`).

If you are very perceptive, you will also have noticed that the sum of a row of Pascal's Triangle is given by `2^(n - 1)`, where n is the row number.

At this time, you are probably asking yourself what this even has to do with the question at hand.

The answer lies in a shortcut to finding your expansion. We must first determine the number of terms that will be inside the expansion of your binomial. In a binomial `(a + b)^n`, the number of terms is given by `n + 1`. Therefore, `(x + 5y)^3` will have `4` terms.

Now, you will have to find the row in Pascal's Triangle that has 4 terms: the numbers in that particular row (the fourth row) are 1, 3, 3 and 1.

Next, in `(a + b)^n`, you must start writing your exponents, from `3`, for a, descending to `0`. For b, write your exponents ascending from 0 to 3. You will do all of this while multiplying the numbers that you found in the fourth row of the Pascal's Triangle. The numbers need to be in order, of course, for this to work.

`(1 xx (x)^3 xx (5y)^0) + ( 3 xx (x)^2 xx (5y)^1) + (3 xx (x)^1 xx (5y)^2) + (1 xx (x)^0 xx (5y)^3)`

`=x^3 + 15x^2 + 75xy^2 + 125y^3`

We received the same answer, except in a lot easier and more concise fashion. As I said earlier, it's a shortcut.

Hopefully this helps!