How do you solve #-3x-2y=0# and #3x-y=18# by graphing?

Question

5353 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-18T06:37:08

From the graphs, the intersection points are #(4,-6)#, so the answer is #x=4# and #y=-6#

standard linear equation is #y=mx+b# format.

#-3x-2y=0#

#-2y=0+3x#

#y=-3/2x" " -> " equation 1 " [color(red)("Red Graph")]#

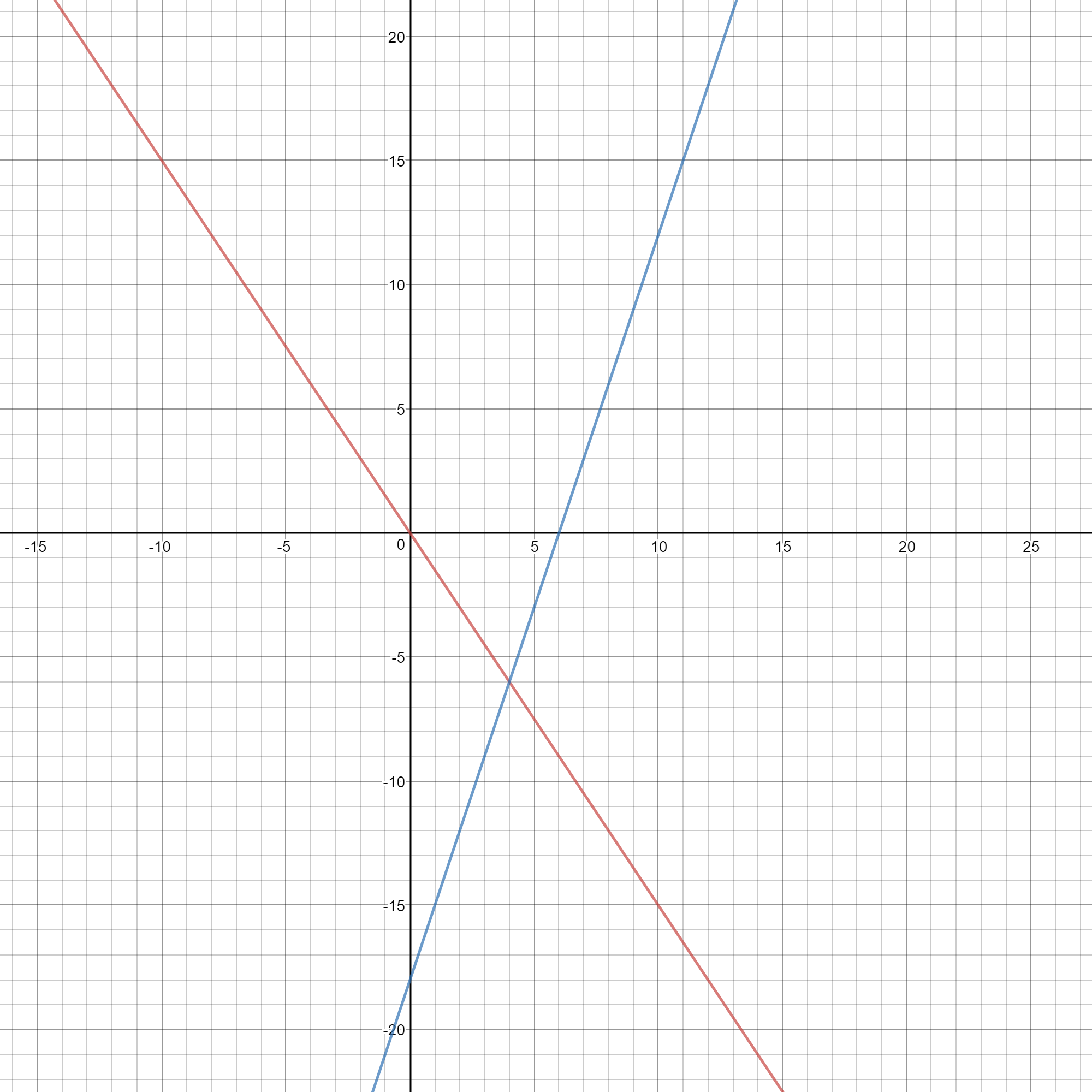
enter image source here

#3x-y=18#

#-y=18-3x#

#y=-18+3x#

#y=3x-18" " -> " equation 2 " [color(blue)("Blue Graph")]#

Now, draw a graph of these linear equations and the intersection of these two graphs is the #(x,y)# point that satisfies both these equations.

From the graphs, the intersection points are #(4,-6)#, so the answer is #x=4# and #y=-6#

Check the answer:

#-3(4) -2(-16) = -12 + 12 = 0#

#3(4) - (-6) = 12 + 6 = 18#