How do you solve a triangle given a=6.3. b=9.4, <C=38.3° ?
1 Answer
Explanation:
Here is what I think the triangle looks like:
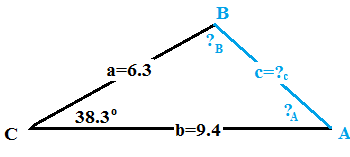
By the Law of Cosines:
using the given values for
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
By the Law of Sines:
with given and determined values
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The conversion of
into
is only valid provided angle A is acute
If a triangle has an obtuse angle, that angle will be opposite the longest side (note there can be at most one obtuse angle).
In other words, if an angle is opposite a side which is not the longest side, that angle must be acute.
It is therefore safe to use the Law of Sines to evaluate
The largest angle (the angle opposite the longest side) should always be evaluated as
