How do you solve a triangle given B=150 degrees, a=10, c=20?

Question

20515 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-26T19:33:21

Draw a diagram to represent the situation.

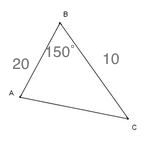
enter image source here

We have to start by finding side B with cosine's law.

#b^2# = #a^2# + #c^2# - 2ac(#cosb#)

#b^2# = #10^2# + #20^2# - 2(10)(20)(cos150)

#b^2# = 846.4101615...

b = 29.093

Now, we can use Sine's law to solve for angles A and C

#(sinA)/a# = #(sinB)/b# = #sinC/c#

#sinA/10# = #sin150/29.093#

A = 9.896˚ = 10˚

B = 180 - 150 - 10

B = 20˚

So, b = 29.093, A = 10˚ and B = 20˚.

Exercises:

Solve each triangle. Round angles to the closest degree and sides to the nearest thousandth. Beware of the ambiguous case of the Sine's

a) a = 29 cm, b = 34 cm and c = 15 cm

b) A = 27˚, b = 44 cm et c = 25 cm

c) a = 57 cm, b = 48 cm, B = 86˚

Good luck!