Question

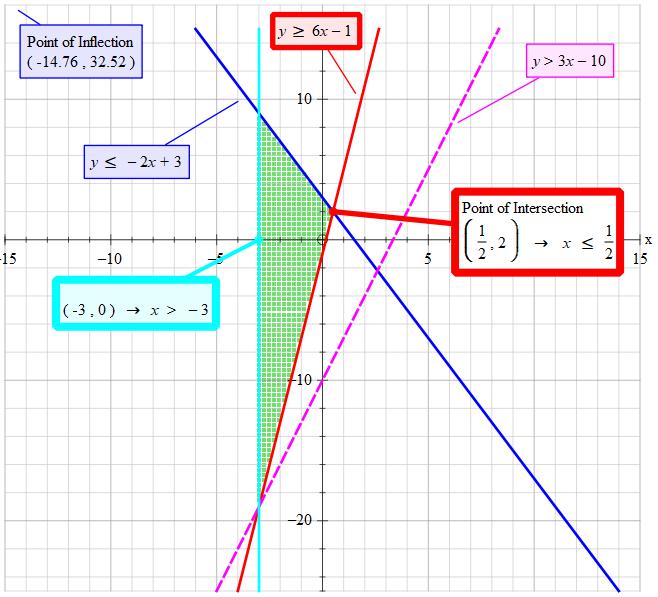
How do you solve and graph `-2a+3>=6a-1>3a-10`?

Answer 1

Answer is `-3 < a<=1/2`

Explanation:

`-2a+3>=6a-1>3a-10`

means `-2a+3>=6a-1`

i.e. `3+1>=6a+2a`

or `8a<=4` i.e. `a<=1/2`

Also `6a-1>3a-10`

or `6a-3a> -10+1`

or `3a> -9` i.e. `a> -3`

Hence answer is `-3<a<=1/2`

Answer 2

`-3 < a <= 1/2`

Explanation:

`color(blue)("Consider: "-2a+3>=6a-1)`

Add `2a` to both sides

`3>=8a-1`

Add 1 to both sides

`4>=8a`

Divide both sides by 8

`1/2>=a`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Consider: "6a-1>3a-10)`

Subtract `3a` from both sides

`3a-1> - 10`

Add 1 to both sides

`3a > -9`

Divide both sides by 3

`a > -3`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("putting it all together")`

In the same order as in the question.

`1/2>=a > -3`

Lets 'rotate' it horizontally `180^o`

`color(red)("THE SOLUTION "-> bar(ul(|color(white)("d")-3 < a <= 1/2color(white)("d") |)))`

You use a 'hollow' circle at the end for 'greater than' or 'less than'.

You use a 'filled in' circle at the end for 'less than or equal to' or 'greater than or equal to'.

`~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`

`color(blue)("IF YOU WERE TO PLOT THESE AND ASSIGN THE VALUES TO y")`

The feasible region for `y` is the shaded area

To construct this I used:
`ubrace(-2a+3>=6a-1>3a-10)`

`-2x+3>=y>3x-10`

AND

`ubrace(-2a+3>=6a-1>3a-10)`
`color(white)("dddddd")y>=6x-1`

`y<=-2x+3`
`y>=color(white)(-)6x-1`
`y>color(white)(-)3x-10`

`x>=-3 larr" Needed to control the lower bound of "a`