How do you solve and graph the compound inequality #3x > 3# or #5x < 2x - 3# ?
1 Answer
Solution:
Interval Notation:
Explanation:
We are given the inequality expression:
Since the
Solve the inequality expressions separately:
Divide both the sides of the inequity by
Subtract
Divide both sides of the inequality by
Hence, the final solutions:
Interval Notation:
Represent the solution on a graph:
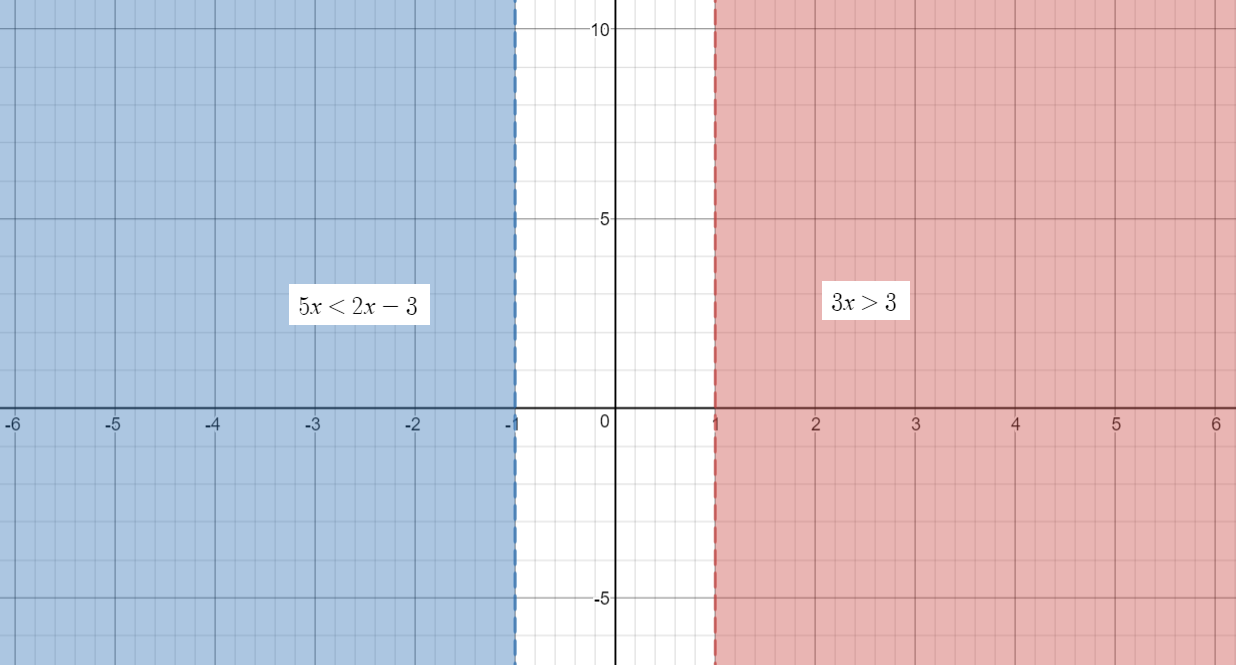
Dotted Lines on the graph indicate values that are NOT part of the Solution Set.
Hope it helps.

