How do you solve by graphing #y = 4x + 4# and #3x + 2y = 12#?

1 Answer
Alan P.
May 29, 2015

A graph of the given equations (see below) may give an indication of the general area of the solution; but (unless it is drawn at a very large scale) it is unlikely to provide an exact solution.

Both equations are linear and the easiest point to evaluate are the x and y intercepts

#y = 4x+4#
#color(white)("XXXX")# has a y-intercept at #(0,4)# and an x-intercept at #(-1,0)#

#3x+2y=12#
#color(white)("XXXX")# has a y-intercept at #(0,6)# and an x-intercept at #(4,0)#

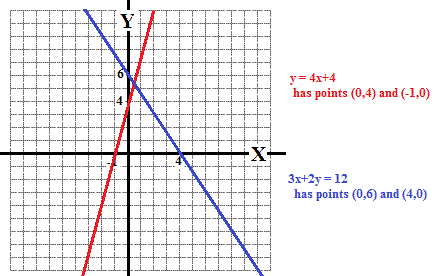
enter image source here

Using analytic methods (non-graphing) give the solution
#(x,y) = (4/11,60/11)#

Related questions
See all questions in Graphs of Linear Systems
Impact of this question
6754 views around the world
You can reuse this answer
Creative Commons License