There are several ways to solve this:
Algebraically
If #x^2 >= abs(x)#
then we can examine the two cases:
#{:
("if "x >=0,x^2>=abs(x)rarr,x^2 >=x,color(white)("xxxx"),"if "x <0,x^2 >=abs(x)rarr,x^2>=-x),
(,,,,x >=1,,-x >= 1),
(,,,,,,x <=1)
:}#
Graphically
Compare the graphs of #x^2# and #abs(x)# for the ranges where #x^2>=abs(x)#
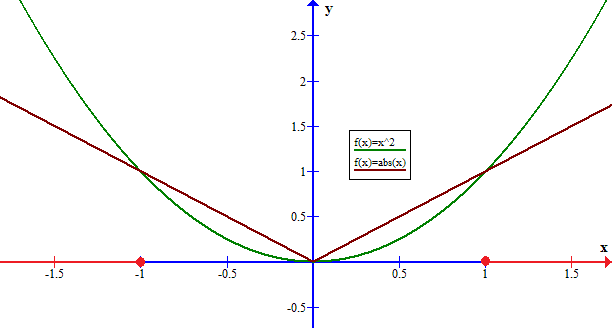
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since the solution is a union of two ranges we use the #uu# symbol to connect our specification of each range.
The range for #x < 0#
extends to #-oo# ...but this is not a real value, only a limit, so we use the "open" parenthesis to show that it is not really included: #(-oo#
and
includes #-1# ...where #-1# is part of the solution, so we use the "closed" parenthesis to show that it is included: #-1]#
Similarly for the # x >= 0# range notation.

