How do you solve the system by graphing #2x + 4y =2# and #x + 2y = 1#?
1 Answer
See below...
Explanation:
To solve this we must graph each of the lines:
First line:
Rearange:
Now we need to plot two or three points that lie on the line:
We need to find
At
At
Hence these are two points that lie on the line:
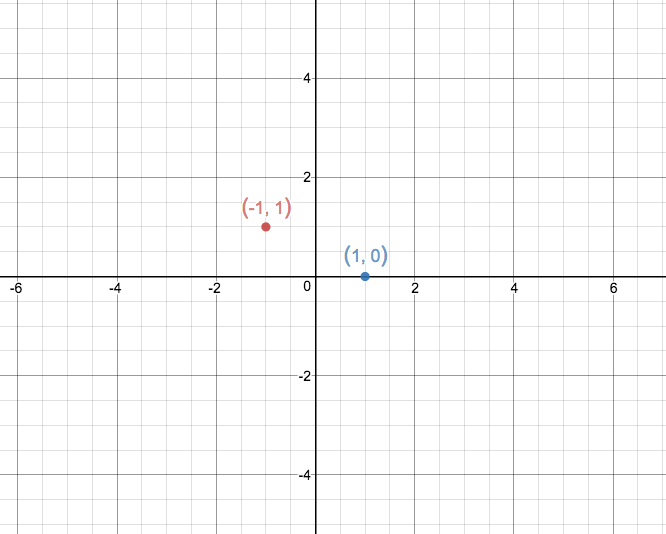
Hence connecting them up to give a line:
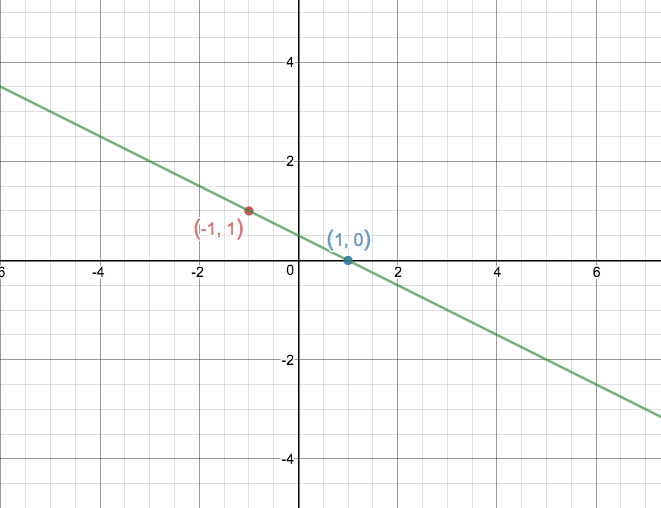
Now we can do this whole procces for the second line, graphing them on the same graph we see:
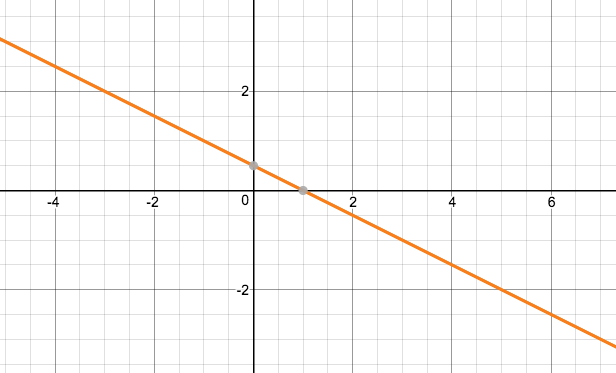
When we deal with these roblems, the solution is where the lines intersect, where they meet
They meet at all points, as they are the same:

