Question

How do you solve the system by graphing given `x + y = 4` and `–x + y = 2`? Thanks in advance for any help at all on this one!?

Answer 1

You can give values of `x` and evaluate the corresponding `y` for the two equations.
By plotting the points obtained you'll be able to "see" the point where your lines cross each other:
Have a look:

Answer 2

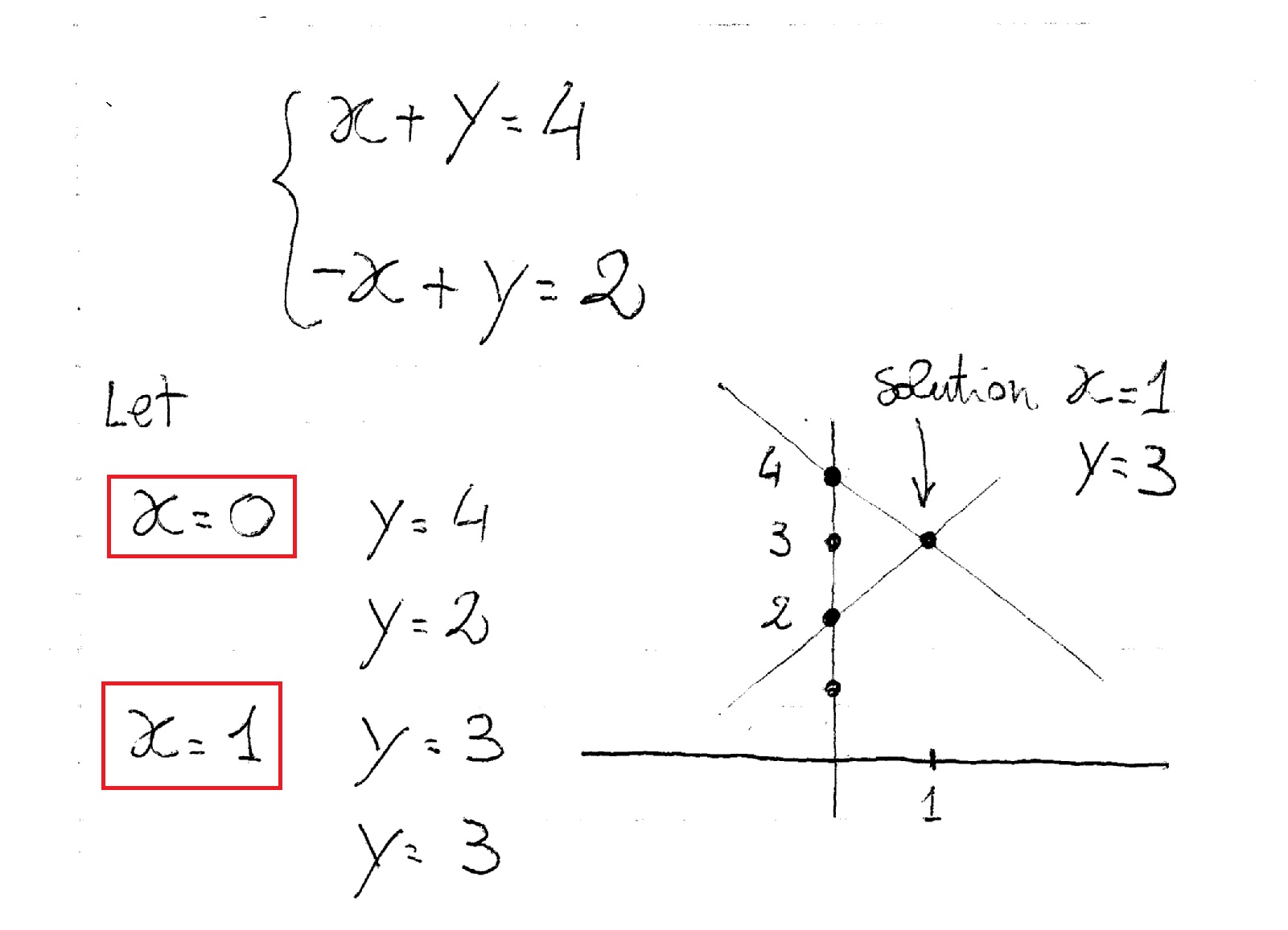
the software here won't let us put two lines on the same garaph, so I'll post them separately and you'll have to put them on one coordinate system:

`x+y=4` is a linear equation. Its graph is a line.
You could get two points and connect the dots.
Or you could solve for `y` to get slope-intercept form:
`x + y=4` subtract `x` (add `-x` on both sides to get:
`y=-x+4`

Graph: graph{y=-x+4 [-6.54, 13.46, -2.64, 7.36]}

Now graph `-x+y=2` which is the same as `y=x+2`

graph{y=x+2 [-6.54, 13.46, -2.64, 7.36]}

Look at the graph to see where the lines intersect.

.

Both lines contain the point `(1, 3)`.

`x=1`, and `y=3` makes both equations true, so it is a solution to the system.