Question

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent `x + y = 4` and `–x + y = 2`?

Answer 1

The equations are consistent.
The point of intersection is `(x,y)->(1,3)`

Explanation:

Given:
`x+y=4`.........................(1)
`-x+y=2`.....................(2)

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Both equations are in the same format. AS such and the fact that the coefficients of `x` (which is 1 and -1) are opposite signs then at some point the will coincide. Thus there exists a single pair of coordinates that will satisfy both equations. Consequently they are consistent.

By sight: Directly adding equations (1) and (2) gives:

`2y=6`

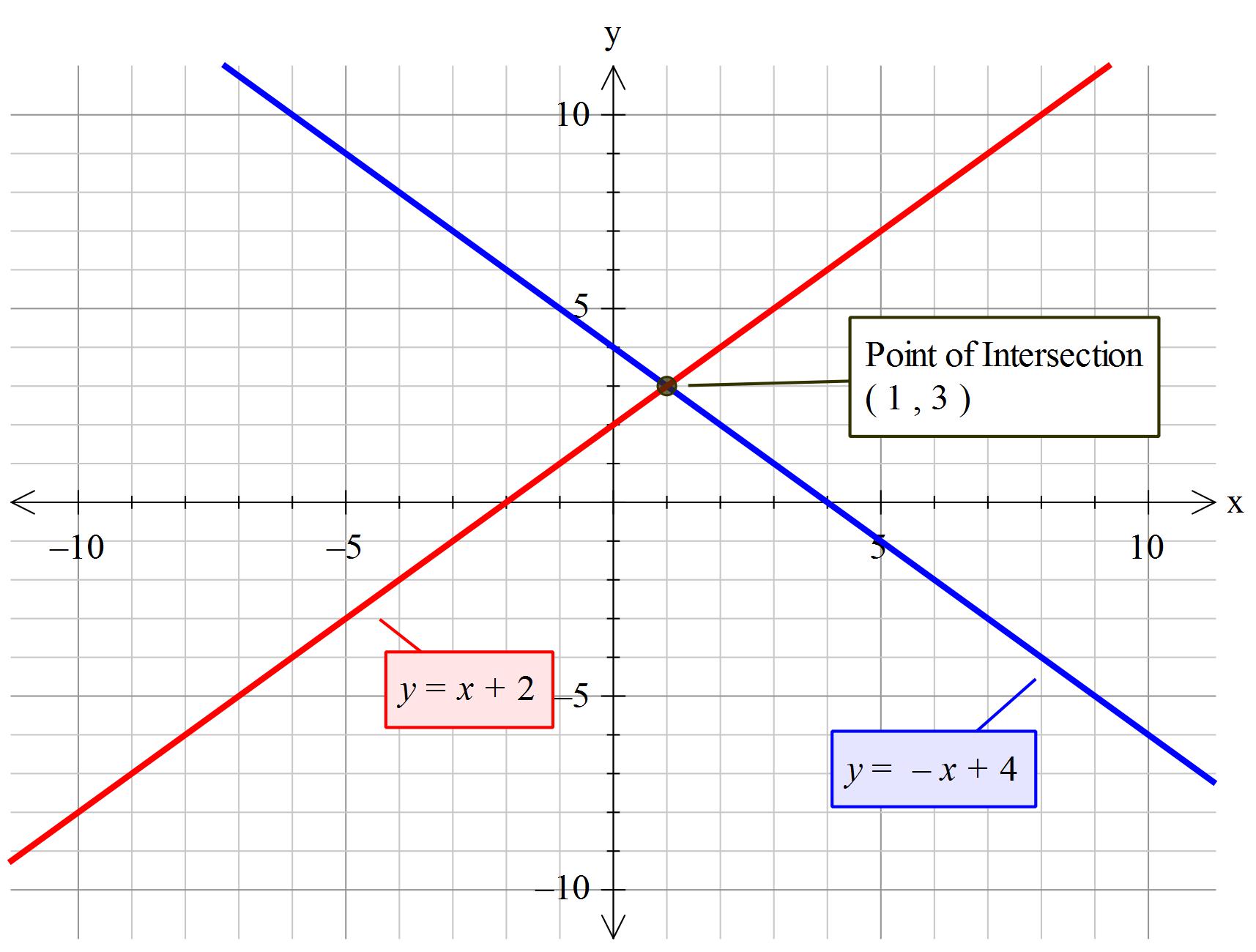
Thus `y=3`

Given that `y=3`, by sight, `x=1`
So the graphs intersect at `(x,y)->(1,3)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~
To graph these write the equations as:
`y=-x+4` .............................(1_a)
`y=x+2`....................................(2_a)

If this is for homework you will be required to produce a table of values for each equation. I would suggest 3 values each