Question

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent `x+y=11`, `x-y=-3`?

Answer 1

The equations are consistent with a single solution `(x,y)=(4,7)`

Explanation:

Using graphing (as requested)

We can be picking arbitrary values for `x` using the equation `x+y=11` we can generate a few (two would actually be enough, but I generated 3 for demonstration purposes) solution points for `(x,y)` on this line:
#color(white)("XXX"){:(ul(x),color(white)("xx"),ul(y)), (0,,11),(5,,6),(11,,0) :}#
Plotting these sample points on the plane and drawing a line through the points, we get a graph of the form:

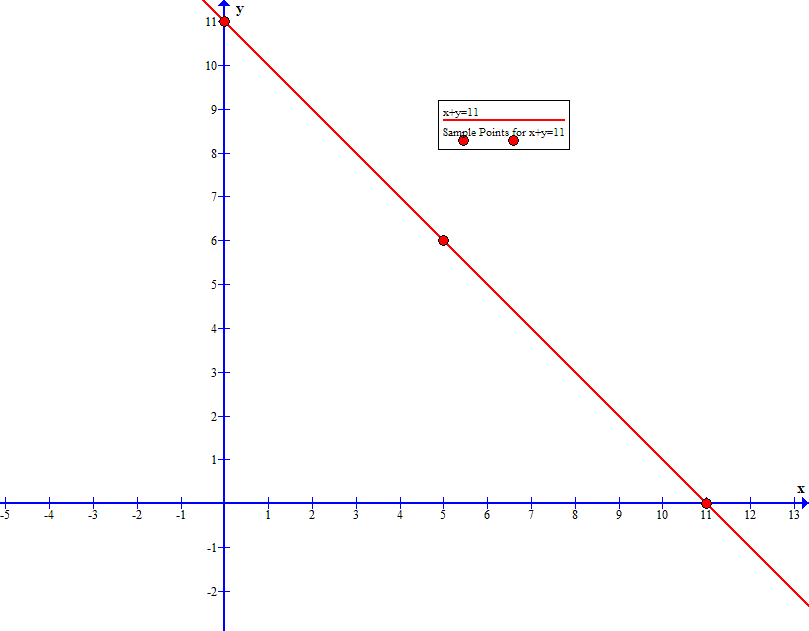
We can repeat this process for `x-y=-3`.
The sample solution points that I generated for this were
#color(white)("XXX"){:(ul(x),color(white)("xx"),ul(y)), (0,,3),(5,,8),(-3,,0) :}#
to generate the graph

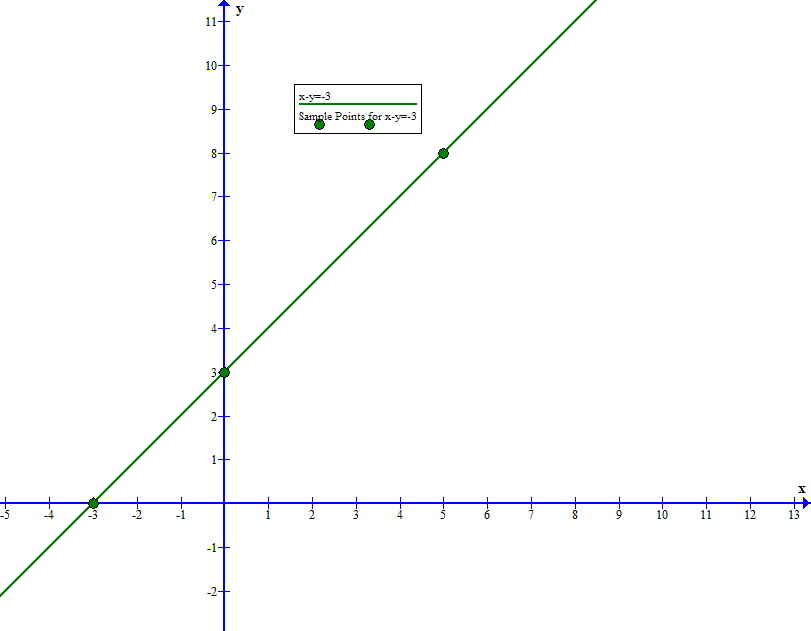
If we combine these graphs on the same plane:

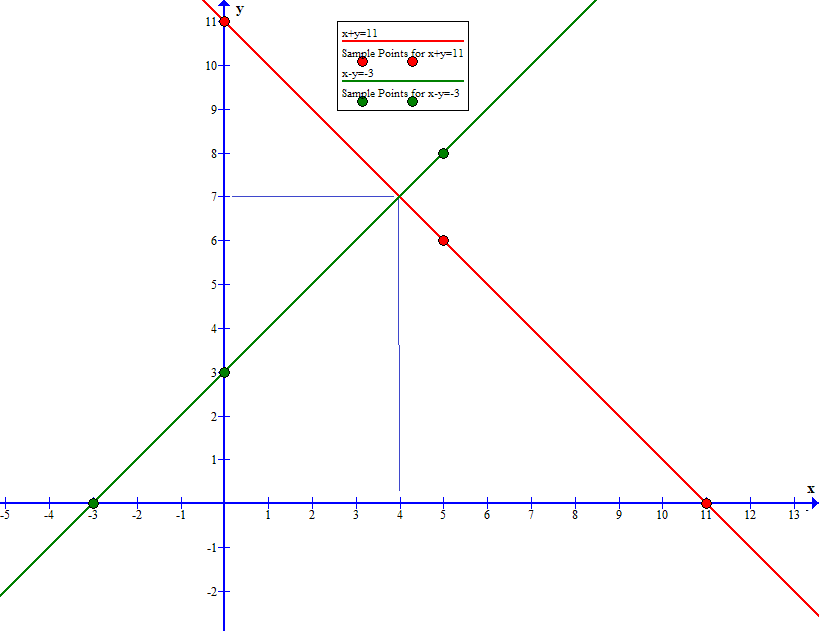
We see that the two lines intersect (and therefore are consistent)
at the coordinates `(x,y)=(4,7)`