Question

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent `3x + y = -3` and `6x - 6y = -30`?

Answer 1

The system is a consistent set of equations with solution at
`(x,y)=(-2,3)`

Explanation:

Since both given equations are linear
we only need 2 coordinate pairs for each to establish their lines.
(We can pick any values for one variable and solve for the other to find these points).

Here are the sample points I used:
#{: (color(green)(3x+y=3),color(white)("xxxx),color(purple)(6x-6y=-30)) :}#
#{: (color(green)(ul(x)color(white)("xxxx")ul(y)),color(white)("xxxxxxxx"),color(purple)(ul(x)color(white)("xxxx")ul(y))), (color(green)(0color(white)("xxx")-3),,color(purple)(0color(white)("xxxxx")5)), (color(green)(-1color(white)("xxxx")0),,color(purple)(-5color(white)("xxx")0)) :}#

Plotting each pair of coordinates and drawing a line through each set gives a graph:

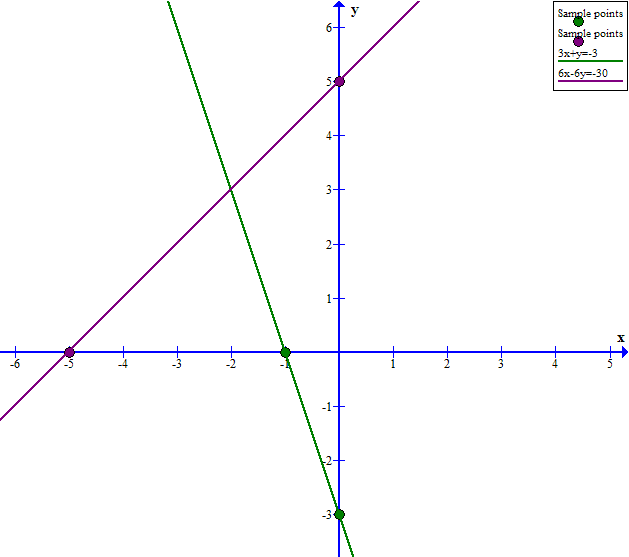
The lines intersect at a single point and therefore are consistent.

Examining the graph, we see that the intersection point happens at
`x=-2` and `y=3`