Question

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent `4x - y = 6` and `3x + y = 1`?

Answer 1

These equations are consistent
and have a solution at `(1,-2)`
`color(white)("XXX")`(see below for method)

Explanation:

For each of the two functions:
`color(white)("XXX")`choose two convenient points on the function;
`color(white)("XXX")`plot and draw a line through the the two points.
The equations are consistent if the lines cross and inconsistent if they do not.
If they are consistent, the point at which they cross will be the solution.

For `color(red)(4x-y=6)`
I chose the points `color(red)("("0,-6")")` and `color(red)("("2,2")")`

For `color(blue)(3x+y=1)`
I chose the points `color(blue)("("0,1")")` and `color(blue)("("-1,4")")`

Plotting the points and drawing the connecting lines, I got:

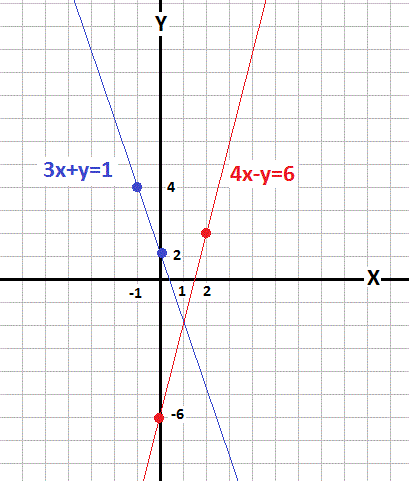
The lines intersect to the equations are consistent

The solution point appears to be at (or close to) `(x,y)=(1,-2)`

(In fact that is the exact solution, but using graphing techniques we can not be absolutely certain of the accuracy).