How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent #4x - y = 13# and #4x + 5y = -17#?
1 Answer
Find two coordinates for each equation that satisfy the equation;
plot the points; draw a line through the two points for each equation; the point of intersection will be the common solution.
Explanation:
Testing various values of
I came up with
#color(green)({: (underline(x),color(white)("XXX"),underline(y)), (0,,-13), (5,,7) :})#
Similarly for
I found as possible solutions:
#color(red)({: (underline(x),color(white)("XXX"),underline(y)), (-3,,-1), (7,,-9) :})#
Plotting each of these pairs of solutions and drawing a line through the pair of points for each gives:
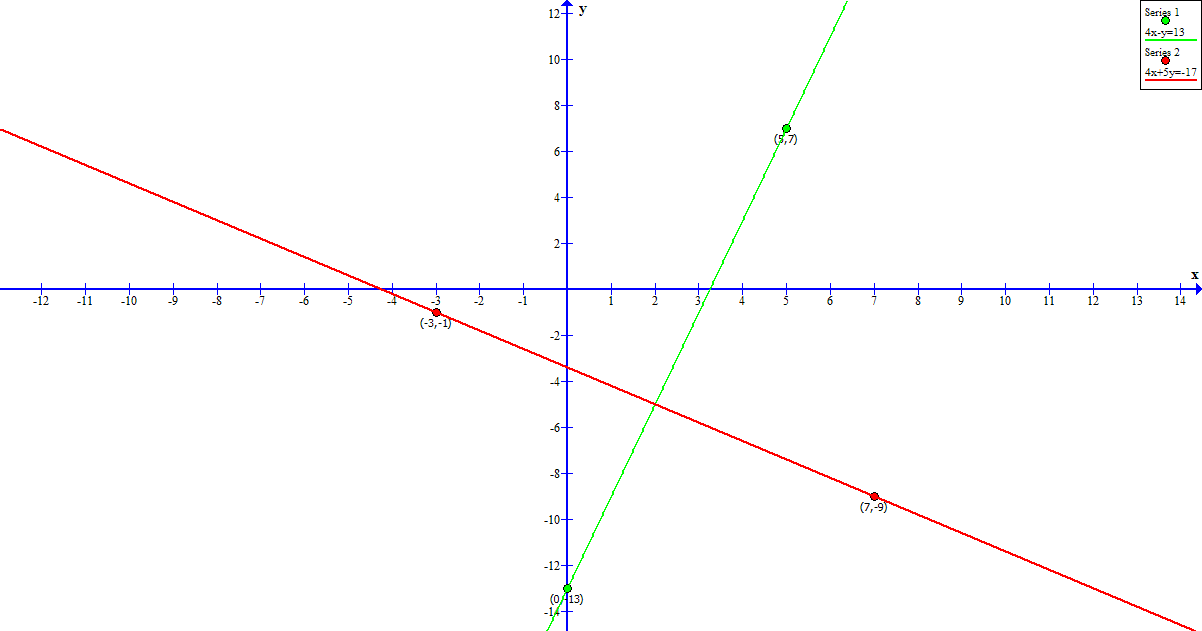
Since the lines intersect, the equations are consistent
with an apparent solution at
