Question

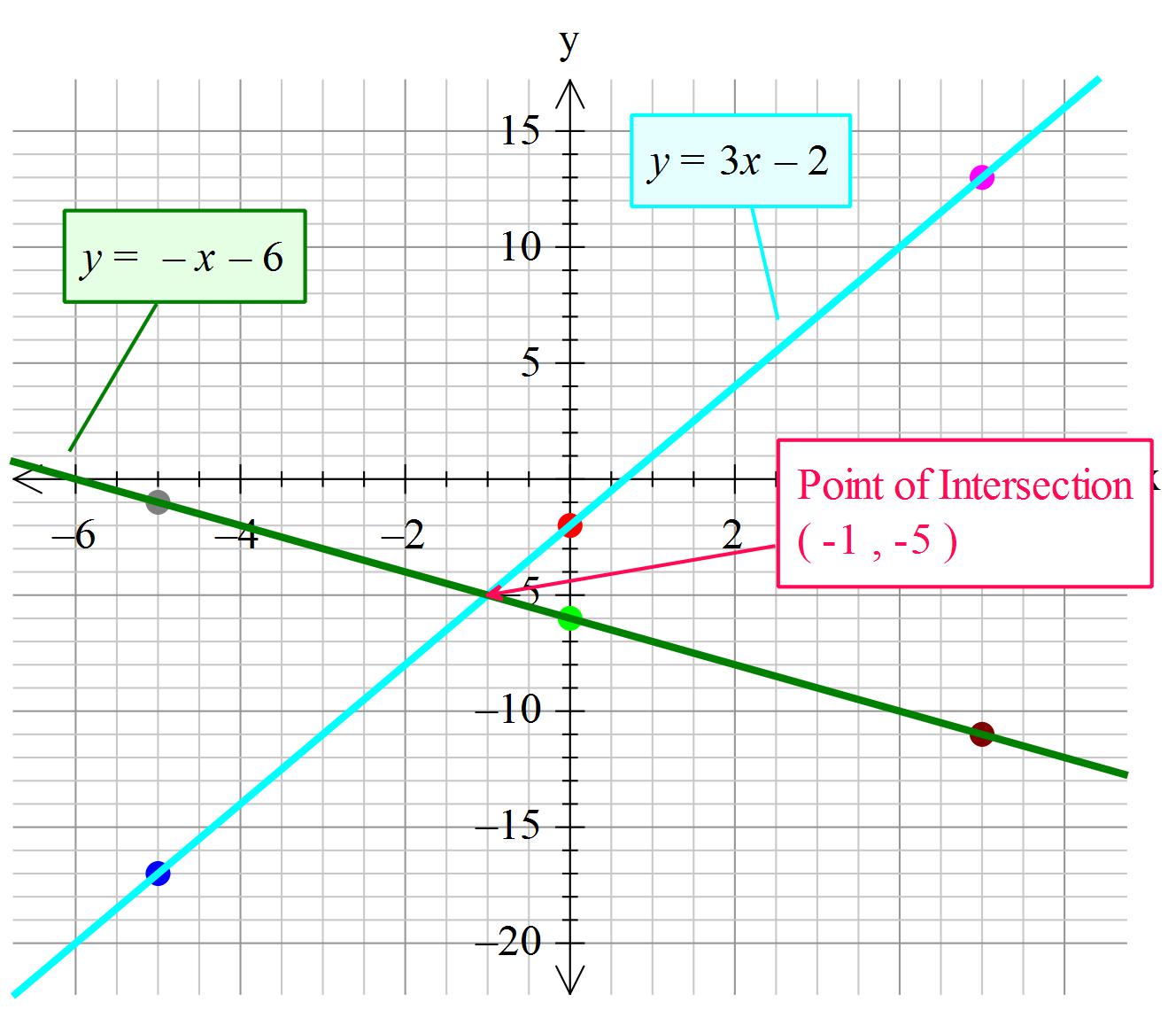
How do you solve the system of equations by graphing `y=3x-2`, `x+y=-6`?

Answer 1

The common value are `(x,y)->( -1,-5 )`

Explanation:

Given:
`" "y=3x-2`...................... Equation (1)
`" "x+y=-6` ......................Equation (2)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Changing the form of equation (2) so that it matches eqn type `y=mx+c`

Subtract `color(blue)(x)` from both sides

`=>color(brown)(x+y=-6" "->" " x color(blue)(-x)+y=-6color(blue)(-x)`

But `x-x=0`

`0+y=-x-6`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So now we have both equations in standard form

`y=3x-2color(white)(.) ............................(1)`

`y=-x-6color(white)(.).........................(2_a)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Make a table of values that outputs the value of `y` for your chosen values of `x`

For example

Plot your points and draw lines through them extended to the edge of the squares.

Mark your points and label each line to show which equation it represents.

The point where the two lines cross is the solution. ie the x value and the y value

If all three points for any one of the lines do not line up then your point calculations are wrong some where.