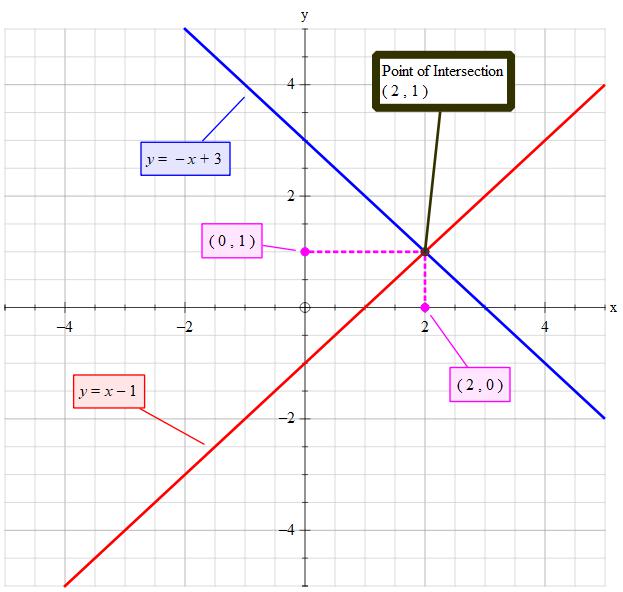
#color(blue)("Consider: "x+y=3)#
Subtract #x# from both sides
#+x+y=3#
#ul(-x color(white)("dddddddd")- x)#
#color(white)("d.")0+y=3-x#
#color(white)("dddddddd")color(red)(ul(bar(|color(white)(2/2)y=-x+3color(white)(2/2)|)))#
The line crosses the x-axis at #y=0 =>0=-x+3 =>x=3#
So we have #x_("intercept")->(x,y)=(3,0)#
The line crosses the y-axis at #x=0=>y=0+3#
So we have #y_("intercept")->(x,y)=(0,3)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Consider: "x-y=1)#
Add #y# to both sides
Subtract 1 from both sides
#x-y color(white)("dddd")=color(white)("dddd")+1#
#ul(color(white)(x)+y-1color(white)("dddd")+y-1)#
#x+0-1color(white)("d") =color(white)("ddd") y+0#
#color(white)("dddddddd")color(red)(ul(bar(|color(white)(2/2)y=x-1color(white)(2/2)|)))#
The line crosses the x-axis at #y=0=> 0=x-1 =>x=1#
So we have #x_("intercept")->(x,y)=(1,0)#
The line crosses the y-axis at #x=0=>y=0-1#
So we have #y_("intercept")->(x,y)=(0,-1)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~