Let us graph the circle #x^2+y^2=36#, which is a circle with center #(0,0)# and radius #6# and #x^2+y^2<36# is the set of all points lying inside the circle but not on the circle, as we have inequality. It would have included points on the circle had the inequality been #x^2+y^2<=36#. The graph of #x^2+y^2<36#, appears as follows:
graph{x^2+y^2<36 [-14, 14, -7, 7]}
Similarly, #4x^2+9y^2>36# is the graph is the set of all points lying outside the ellipse but not on the circle. Its graph appears as follows:
graph{4x^2+9y^2>36 [-14, 14, -7, 7]}
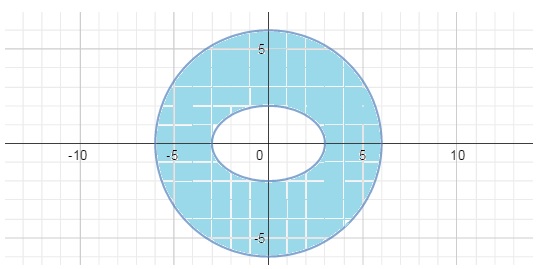
And solution of the system of inequalities #x^2+y^2=36# and #4x^2+9y^2>36# is the set of intersection of points in the two.
Thus it includes points outside the ellipse #4x^2+9y^2=36# but inside the circle #x^2+y^2=36# but does not include points on the circle and the ellipse. The region appears as shown below.