Question

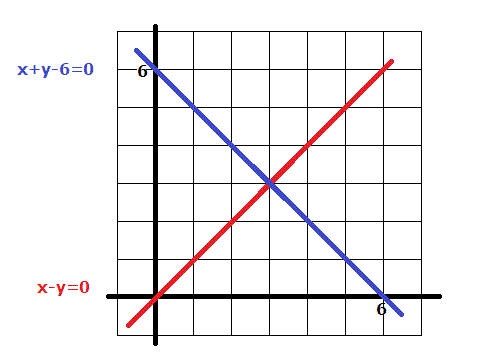
How do you solve the system `x + y - 6 = 0` and `x - y = 0` by graphing?

Answer 1

Draw the lines for the linear equations given and note the point at which the two line insect (in this case at `(x,y) = (3,3)` ).

Explanation:

The easiest points to use for graphing purposes are often the intercepts.

For `color(blue)(x+y-6=0)`
the intercepts are at `(color(blue)(0,6) )` and `(color(blue)(6,0))`

For `color(red)(x-y=0)`
the x and y-intercepts are the same point: `(color(red)(0,0))`
so it will be necessary to pick one more point;
since we already have a `6` lets pick `x=6` which given the equation implies `y=6` and we have a second point `(color(red)(6,6))`

Drawing a line connecting
`color(white)("XXX")(color(blue)(0,6))` and `(color(blue)(6,0))`
and another connecting
`color(white)("XXX")(color(red)(0,0)` and `(color(red)(6,6))`
gives us a point of intersection at `(color(green)(3,3))`