Question

How do you solve the system `y=1/2x+4` and `y=-4x-5` by graphing?

Answer 1

The equations are in standard form, `y=mx+c`, where `m` is the slope (gradient) and `c` is the y-intercept. Using this, graph as shown below to find the solution `(-2,3)`.

Explanation:

The solution of this set of simultaneous linear equations is the point where the lines cross.

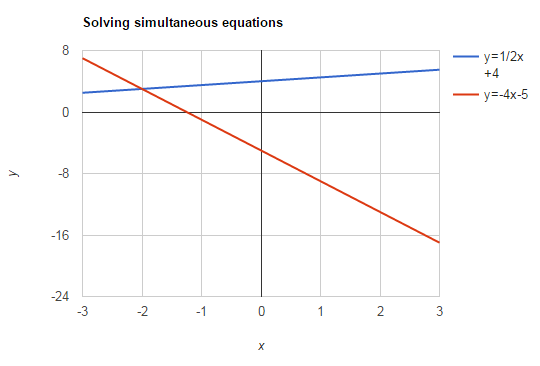
You can read from the graph that this point is `(-2,3)`.

The equations can also be solved algebraically (as a way of checking your answer) by equating the two equations with one another:

`1/2x+4=-4x-5`

Double to make it neater:

`x+8 = -8x-10`

Add `8x` both sides and subtract 8 from both sides:

`9x=-18` which gives `x=-2`

Substitute back into either equation to find `y=3`.