How do you solve the system #y=2x-1#, #6x-3y=12# by graphing?
1 Answer
As the two lines have the same slope, they must be either parallel or coincide with one another.
Explanation:
For the two straight line curves to cut each other, Their slopes must be different. Let us apply this test first.
1st line
#y=2x-1#
Its slope is the coefficient of
2nd equation
It is in the form -
#ax+by=c#
Its slope is defined by#(-a)/b#
#6x-3y=12#
#m_2=(-6)/(-3)=2#
As the two lines have the same slope, they must be either parallel or coincide with one another.
To have an idea about this, Find their respective Y-intercepts.
Y-intercept of the first line is
Y-intercept of the 2nd line is
Since their slopes are the same and intercepts differ, the two lines are parallel to each other.
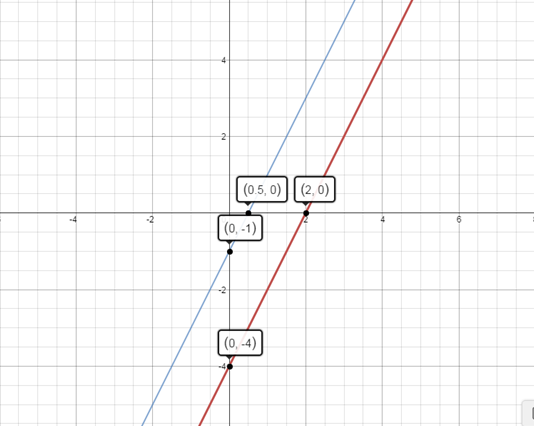
You can find the intercepts of the two lines.
1st line (0, -1); (0.5,0)
2nd line (0,-4); (2, 0)
Fix the two points each for the two lines
The two lines will be parallel to each other.