Determine 2 points for each given equation:
#color(red)(y=2x-4)#
#color(white)("XXX")#using the intercepts:
#color(white)("XXXXXX")(color(red)(0,-4)) and (color(red)(2,0))#
#color(blue)(y=-3x+1)#
#color(white)("XXX")#use the y-intercept
#color(white)("XXXXXX")(color(blue)(0,1))#
#color(white)("XXX")#but the x-intercept is ugly (a fraction),
#color(white)("XXX")#so let's use #x=2# since we already need this #x# value from the first equation.
#color(white)("XXXXXX")(color(blue)(2,-5))#
Plot and join the points for #color(red)(y=2x-4)# and (separately) the points for #color(blue)(y=-3x+1)#
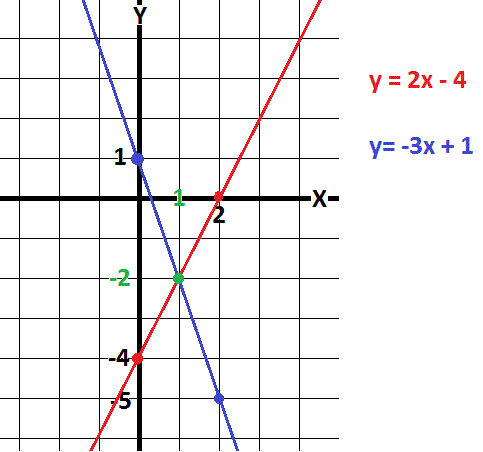
Read the point of intersection directly from the graph as
#color(white)("XXX")(color(green)(1,-2) )#

