How do you solve the #triangle ABC# given #A=50^circ, a=2.5, C=67^circ#?
1 Answer
Aug 5, 2017
See below.
Explanation:
Since all the angles of a triangle sum to
#m /_ A + m /_ B + m /_ C = 180^@#
Substitute in the given information and solve for
#50^@ + m /_ B + 67^@ = 180^@#
#m /_ B + 117^@ = 180^@#
#m /_ B = 180^@ - 117^@#
#m /_ B = 63^@#
We now have the following triangle:
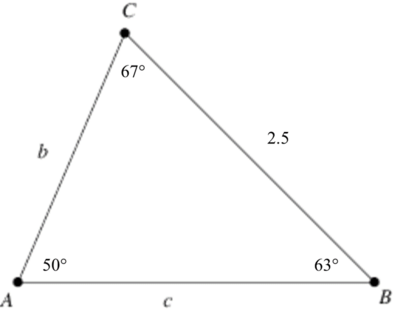
The Law of Sines states that
Thus, we can say
#sin 50^@/2.5 = sin 63^@/b#
Cross-multiply and solve for
#b * sin 50^@ = 2.5 * sin 63^@#
#b = (2.5 * sin 63^@)/sin 50^@#
#b=2.9#
Do the same to find
#sin 50^@/2.5 = sin 67^@/c#
#c * sin 50^@ = 2.5 * sin 67^@#
#c = (2.5 * sin 67^@)/sin 50^@#
#c=3.0#

