Question

How do you solve the triangle given `f=10, g=11, h=4`?

Answer 1

It’s a right triangle.

Measure of the Three angles of the triangle are

`color(blue)(hat F = (pi/2)^c or 1.57^c or 90^@`

`color(red)(hat G = 1.1987^c or 68.68^@`

`color(green)(hat H = 0.3721^c or 21.32^@`

Explanation:

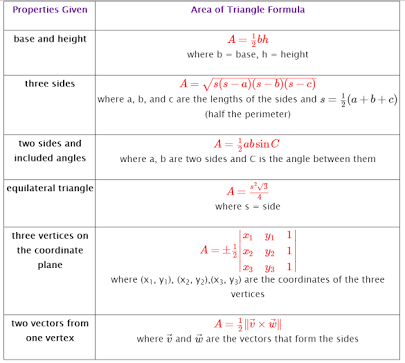
From the table above, having known three sides, we can find the area of the triangle using semi perimeter formula,

`A_t sqrt(s (s-f) (s-g) (s - h))` where s is the semi perimeter of the triangle and

`s = (a + b + c) / 2 = (10 + 11 + 4) / 2 = 12.5`

`A_t = sqrt(12.5 * (12.5-10) * (12.5 - 11) * (12.5 - 4)) ~~ color(brown)(20)`

But we know, `A_t = (1/2) f g sin (hatH)`

`:. sin H = (2 * A_t) / (f * g) = (2*20) /(10*11) = 0.3636`

`hatH = sin^-1 (0.3636) ~~ 0.3721^c`

`sin hatG = (g * sin hatH) / g = (11 * 0.3636) / 4 = 1`

`hat G = sin^(-1) 1 = 90^@ or pi/2^c or 1.57^c`

`hat F = pi - 0.3721 - (pi/2) = 1.1987^c`

It’s a right triangle.