Question

How do you solve using the completing the square method `4x^2 + 4x + 1 = 49`?

Answer 1

`x=-4` or `3`.

Explanation:

`4x^2+4x+1=49` can be written as

`(2x)^2+2xx(2x)xx1+1^2-49=0`

or `(2x+1)^2-7^2=0`

and using `a^2-b^2=(a+b)(a-b)` this becomes

`(2x+1+7)(2x+1-7)=0`

or `(2x+8)(2x-6)=0`

and either `2x+8=0` i.e. `2x=-8` and `x=-8/2=-4`

or `2x-6=0` i.e. `2x=6` and `x=6/2=3`

Answer 2

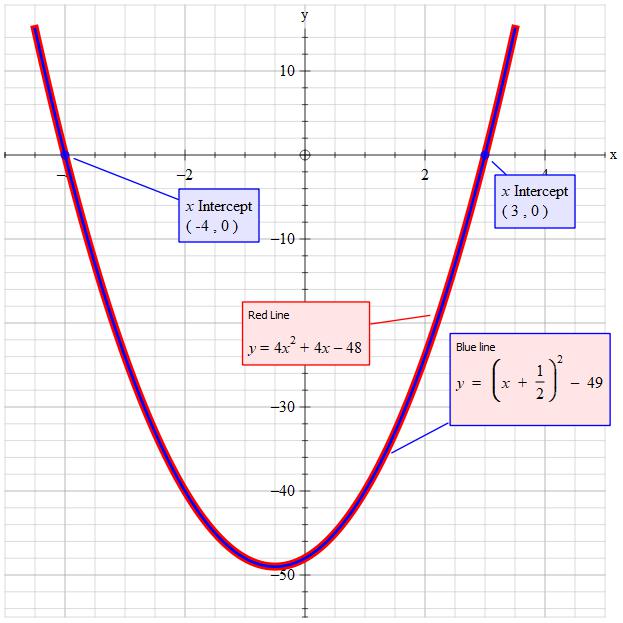
3, and - 4

Explanation:

1. Transforming Method
   `y = 4x^2 + 4x - 48 = 0`
   `y = 4(x^2 + x - 12) = 0`
   Solve the quadratic equation `x^2 + x - 12 = 0`, by the new Transforming Method - case a = 1 (Socratic, Google Search)
   Find 2 real roots, that have opposite signs (ac < 0), knowing the sum (-b = -1) and the product (c = -12).
   They are 3 and - 4
2. Completing the square method.
   `4x^2 + 4x = 48`
   `x^2 + x = 12`
   `x^2 + x + 1/4 = 12 + 1/4 = 49/4`
   `(x + 1/2)^2 = 49/4`
   `x + 1/2 = +- 7/2`
   `x1 = 7/2 - 1/2 = 6/2 = 3`
   `x2 = - 7/2 - 1/2 = - 8/2 = - 4`

Answer 3

`x=-4 and x= 3`

`4(x+1/2)^2-49=0`

Explanation:

Given: `4x^2+4x+1=49" "...................Equation(1)`

Write as:
`4(x^2+4/4 x)+1-49=0 larr` As yet no values have changed.

The next step will change things in as much as it introduces a value that is not in the original equation. It is removed by introducing an as yet unknown constant of `k`. It will turn the introduced value into 0.

`4(x^(color(red)(2))+ubrace(4/4)color(white)("d") x)+1-49=0`
`color(white)("ddddddd")darr`
`color(white)("dddd")"Halve this."`
`color(white)("ddddddd")darr`
`4(xcolor(white)("d")+color(white)("d")1/2color(white)("d"))^(color(red)(2))+k-48=0" "..................Equation(2)`

Notice the exponent `(color(red)(2))` has been moved outside the bracket, the `x` from `4/4 x` has been removed and that `k` has been introduced. Also as indicated, the `4/4` has been halved as well.

`color(brown)("The above set of steps form the basis for completing the square")`

Now we do the correction bit.

Set `4(1/2)^2+k=0color(white)("ddd")=>color(white)("ddd") 1+k=0color(white)("d")=>k=-1`

Substitute into `Equation(2)` giving:

`4(x+1/2)^2-1-48=0`

`4(x+1/2)^2-49=0 larr`Completed square form
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Add 49 to both sides

`4(x+1/2)^2=49`

Divide both sides by 4

`(x+1/2)^2=49/4`

Square root both sides

`x+1/2=+-7/2`

Subtract `1/2` from both sides

`x=-1/2+-7/2`

`x=-4 and x= 3`