How do you solve #-(x+2)^2<=0#?
2 Answers
Dec 16, 2017
Explanation:
We can do this a couple of ways:
- By observation, see that the smallest value on the LH side is attained with
#x=-2# (since the term inside the bracket is squared, it cannot return a negative value). And so every term coming from the squaring of the bracket will be at least 0. The negative sign, then, will make every term no bigger than 0. This means that there is no#x# that will make the LH side bigger than 0.
#:. x in RR#
- With algebra
Multiply by
Take the square root of both sides:
or
Dec 16, 2017
We can validate this with a sketch:
Explanation:
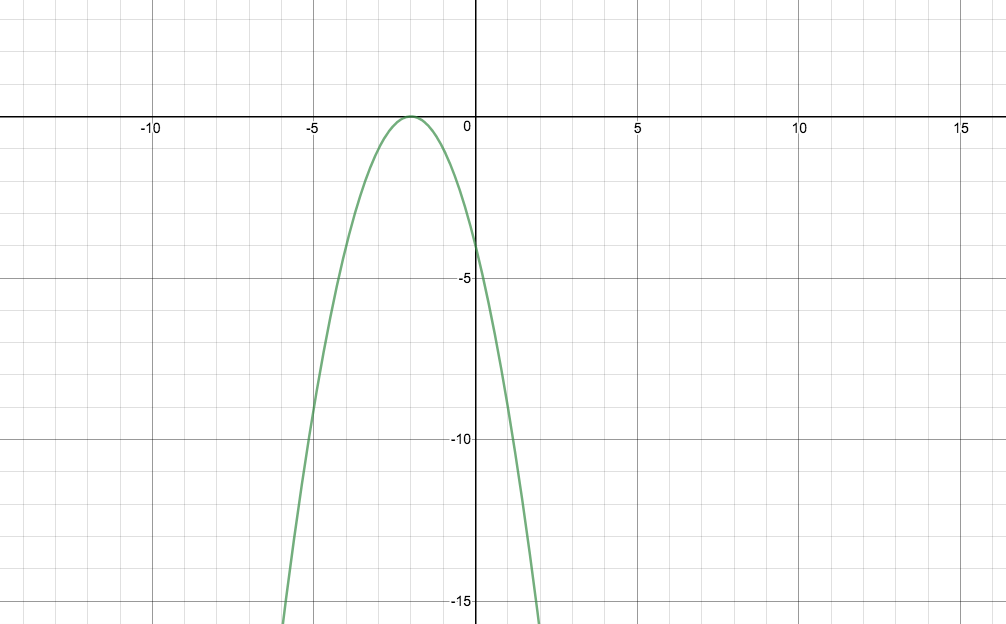
We see its always negative


