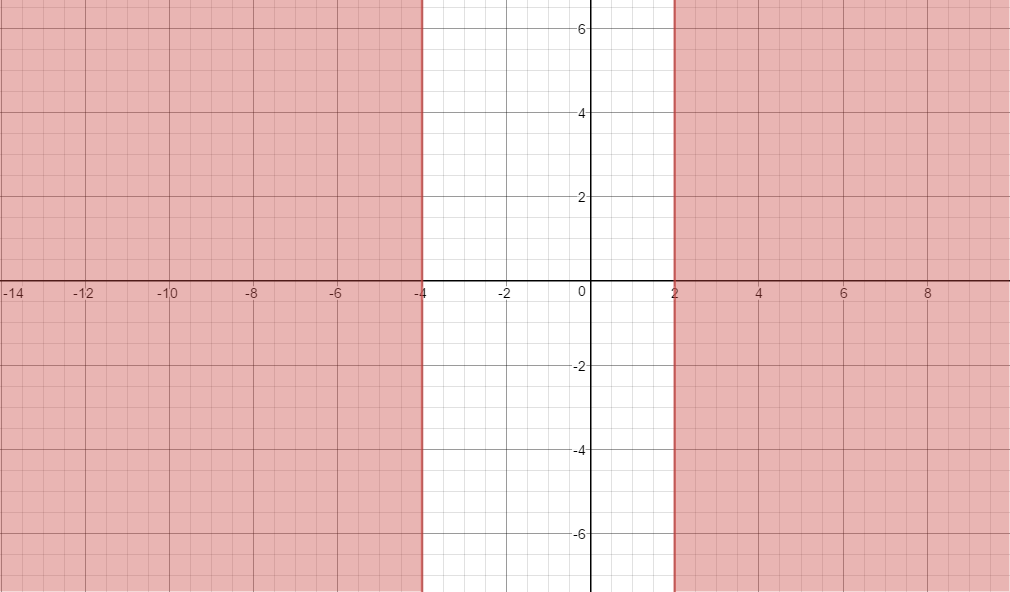
How do you solve #-x^2-2x+8<=0# by graphing?

Question

2958 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-10-04T02:12:16

Write this as follows

#-x^2-2x+8<=0#

#x^2+2x+1-1-8<=0#

#(x+1)^2-3^2<=0#

#(x+1+3)*(x+1-3)<=0#

#(x+4)*(x-2)<=0#

Hence the solutions for the inequality are

#x>=2# and #x<=-4#

A graphical representation can be seen on the figure below

enter image source here