If we use the quadratic formula to factor color(red)1x^2color(blue)(-3)xcolor(green)(-32)
we find zeros at
color(white)("XXX")x=(-(color(blue)(-3))+-sqrt((color(blue)(-3))^2-4 * color(red)1 * (color(green)(-32))))/(2 * color(red)1)
color(white)("XXXX")=(3+-sqrt(137))/2
giving the factors:
color(white)("XXX")x^2-3x-32 =(x-(3+sqrt(137))/2) * (x - (3-sqrt(137))/2)
x^2-3x-32 will be greater than zero if and only if
{:
("both terms are positive","or","both terms are negative"),
(x>(3+sqrt(137))/2,,x < (3-sqrt(137))/2)
:}
If you like you could use a calculator to evaluate these irrational expressions:
x > 7.352349955color(white)("XX")orcolor(white)("XX")x < -4.35234995
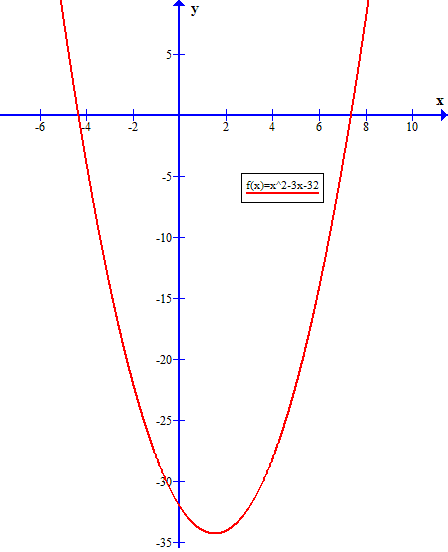
We could verify that these results are reasonable by examining the graph of x^2-3x-32 and noting the values of x for which the graph (y) is above the X-axis: