Given
#color(white)("XXX")(-x-3)/(x+2) <= 0#
Provided #x!=-2# we need to consider two possibilities:
Case 1. If #color(black)(x < -2)#
Since #(x+2) < 0# we need to reverse the inequality when dividing by #(x+2)#
#color(white)("XXX")-x-3 >= 0#
#color(white)("XXX")-x >= 3#
#color(white)("XXX")x <= -3#
#color(white)("XXX")#Considering the two restrictions #x < -2# and #x <= -3#
#color(white)("XXX")#we employ the more restrictive:
#color(white)("XXXXXX")color(green)(x <=-3)#
Case 2. If #color(black)( x > -2)#
Since #(x+2) > 0# we can divide by #(x+2)# without effecting the inequality
#color(white)("XXX")#then -x-3 <= 0#
#color(white)("XXX")-x <= 3#
#color(white)("XXX")x >= -3#
#color(white)("XXX")#Again considering the two restrictions #x > -2# and #x >= -3#
#color(white)("XXX")#we employ the more restrictive
#color(white)("XXXXXX")color(green)(x > -2)#
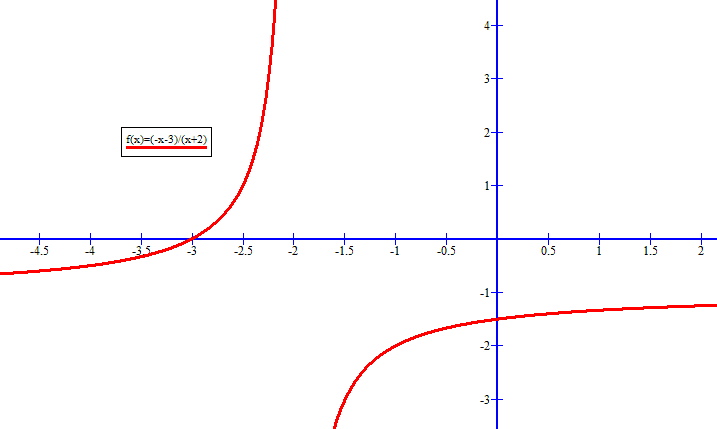
Here is a graph of the #(-x-3)/(x+2)# to help verify this result: