Question

How do you solve `y=x-4`, `2y=-x+10` by graphing and classify the system?

Answer 1

The (shared points) point of intersection is at `(x,y)->(6,2)`.

The system is of type: first order simultaneous equation system

Explanation:

For each equation:
Select at least 2 values for `x` and substitute into the equations to determine the corresponding values of y. Draw a line through each point extending it to the edge of the squares on the graph paper.

`color(blue)("Label all your points and put a title on your graph. Gives you extra")` `color(blue)("marks for good communication.")`

Equation 1
`y=x-4`

Equation 2
`2y=-x+10" "color(red)(vec("divide both sides by 2"))" " y=-x/2+5`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The system is a first order simultaneous equation system

Note:
`x->"first order"`
`x^2->"second order"`
`x^3->"third order"`

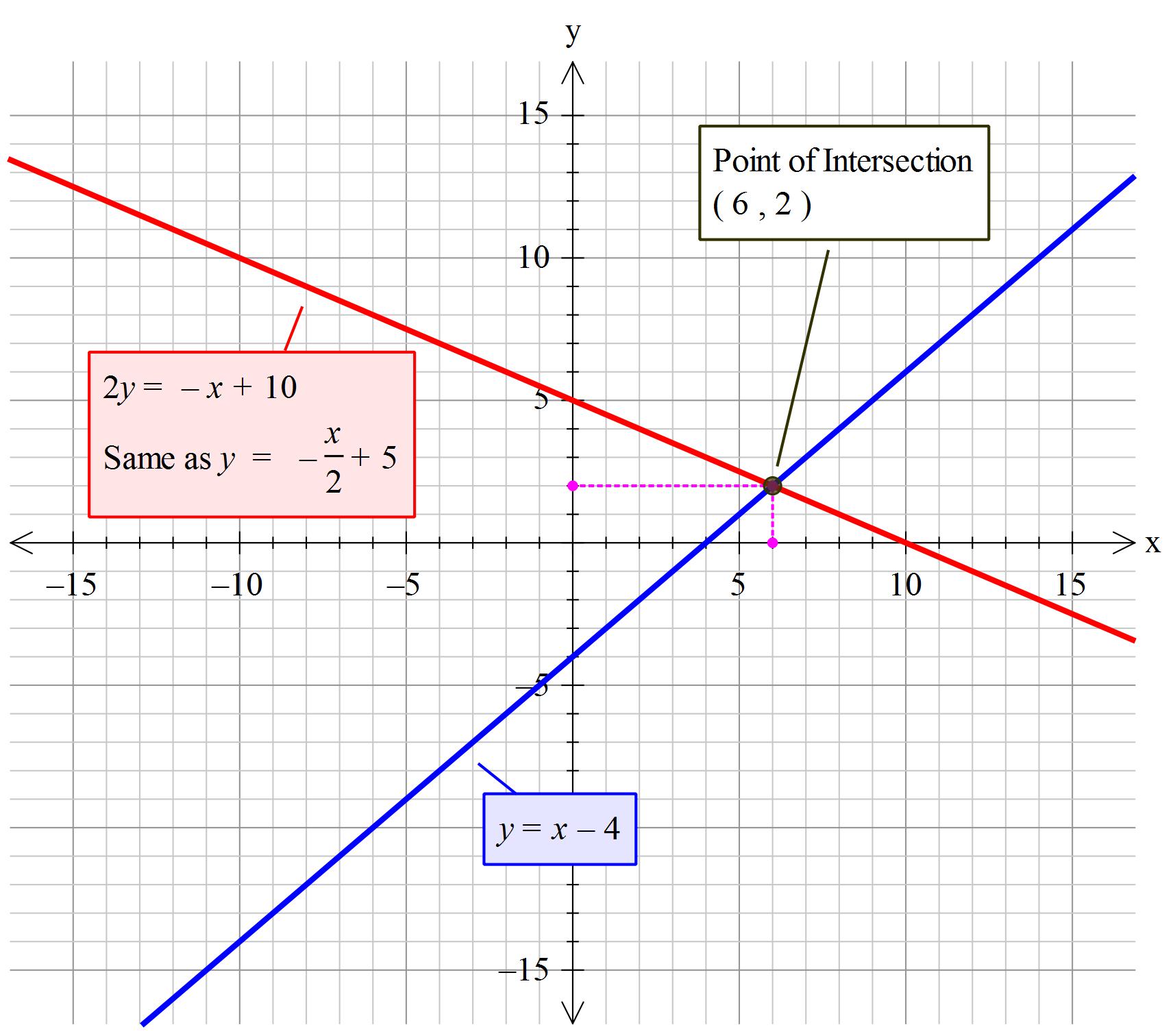
Solution: The (shared points) point of intersection is at
`(x,y)->(6,2)`. The system is a first order simultaneous equation system