Question

How do you tell whether the graph opens up or down, find the vertex, and find the axis of symmetry given `y=1/2x^2+x-2`?

Answer 1

The graph (the Parabola) Opens Up, as the coefficient of `x^2` term is greater than ZERO.

Vertex `= (-1, -2.5)` and Axis of Symmetry `x = -1` Graph attached for a visual proof.

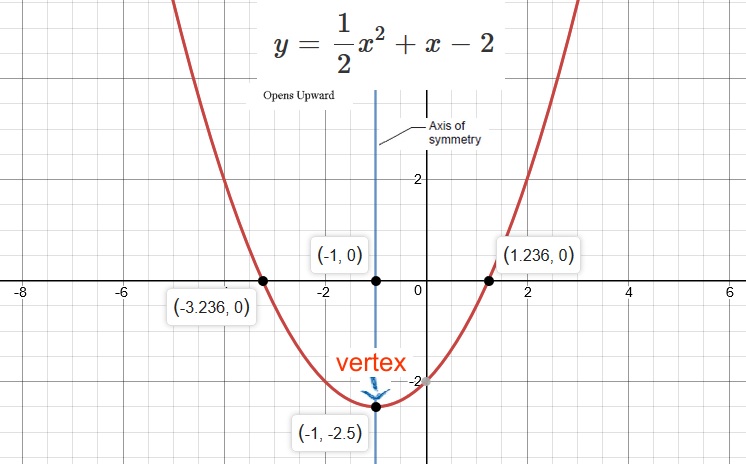
Explanation:

Standard Form of a Quadratic Equation is given by
`ax^2 + bx + c = 0`

If `a > 0` then the Parabola will "Open Up". If `a < 0` then the parabola will "Open Down".

Since in our Quadratic Equation, the coefficient of the `x^2` term is found to be `>0`, the Parabola "Opens Upward".

Also observe that, if the Parabola "Opens Upward" then our Vertex will be a "Minimum" of the Quadratic Function.

We are given the Quadratic Function `y = (1/2)x^2 + x - 2`

The expression `(-b/(2a))` will give us the x-coordinate value of the Vertex.

To obtain the y-coordinate value of the "Vertex", substitute the value obtained from using the expression `(-b/(2a))` in our original equation.

Hence, `y = (1/2)(-1)^2 + (-1) -2` will help us to get the y-coordinate value of the Vertex.

After simplification, we get `y = -2.5`

Hence our Vertex`= (-1, -2.5)`

And our Axis of Symmetry `x = -1`

Please refer to the attached graph for a visual proof of our solution.

I hope this explanation is helpful.