How do you use Heron's formula to determine the area of a triangle with sides of that are 4, 7, and 8 units in length?
1 Answer
Plug in your calculator...
Explanation:
Heron formula requires you know only the sides of a triangle to compute the area. Note you can use another approach i.e. determine the height of the triangle and use our familiar:
Where
There is an elegant prove to this leveraging trigonometry and using the following identities:
Try to complete the derivation...
You can also leverage "Pythagorean Theorem" on the following triangle... see image: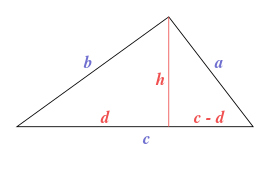
The idea is to express d and h only in terms of:

