How do you use integrals to find the area bounded by the curve y = (x^2 - 9) and the x-axis for x = 0 to x = 5?
1 Answer
Jul 27, 2015
I found: area
Explanation:
You write it as:
you can break it into two as:
integrating you get:
now you use you extremes of integration substituting them and subtracting the resulting expressions as:
You may wonder about the negative sign but looking at your area:
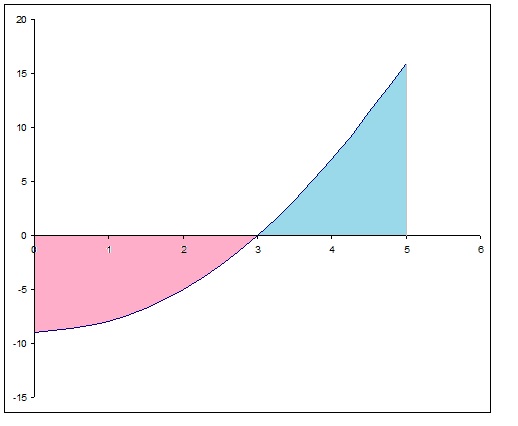
you can see that quite a big chunk (pink) is below the

