Question

How do you use pascals triangle to expand `(x^2 - 2)^4`?

Answer 1

The following diagram shows Pascal's Triangle .

Explanation:

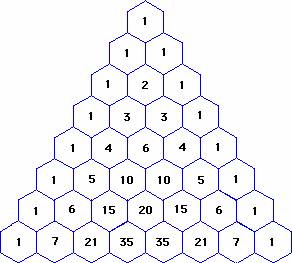
What do you notice?

-The numbers in each column down from the first is the sum of the two numbers above it.

This is important, because to expand a binomial, we need this property.

`(x^2 - 2)^4 => 5` terms, since to find the number of terms you always add 1 to the exponent.

For 5 terms, you must pick the row with 5 terms in the Pascal's Triangle. The row with 5 terms is 1, 4, 6, 4 and 1.

We must multiply these numbers with exponents starting at 4 and ending at 0 for `x^2` and start at 0 and ending at 4 for `-2`. We do that since the total exponent of the expression is 4, and if you include the 0th term, you have your 5 terms.

`(x^2 - 2)^4 = 1(x^2)^4(-2)^0 + 4(x^2)^3(-2)^1 + 6(x^2)^2(-2)^2 + 4(x^2)^1(-2)^3 + 1(x^2)^0(-2)^4`

=`x^8(1) + 4(x^6)(-2) + 6(x^4)(4) + 4(x^2)(-8) + 16`

=`x^8 - 8x^6 + 24x^4 - 32x^2 + 16`

So, `(x^2 - 2)^4 = x^8 - 8x^6 + 24x^4 - 32x^2 + 16`

Practice exercises:

1. Expand the following using Pascal's Triangle.

a) `(2x - 5y)^5`

b) `(y^2 + 2x^2)^7`

Challenge problem:

Expand `(2x - 3y)^-4` using Pascal's Triangle. Hint: remember the exponent rule about how to turn a negative exponent into a positive exponent!

Good luck!