Question

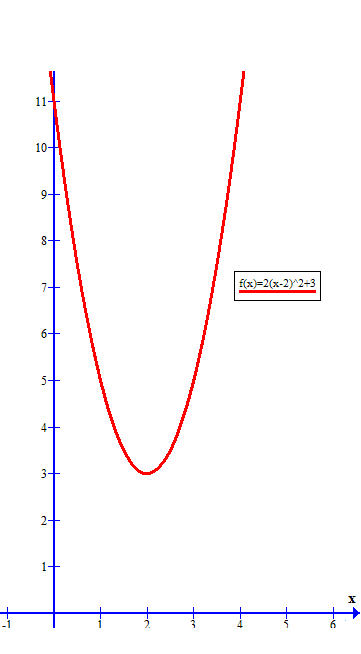
How do you write a quadratic equation with vertex; ( 2,3 ); point: ( 4,11 )?

Answer 1

`y=2(x-2)^2+3`

Explanation:

The general vertex form for a quadratic is
`color(white)("XXX")color(brown)y=color(green)m(color(orange)x-color(red)a)^2+color(blue)b`
with vertex at `(color(red)a,color(blue)b)`
and a "spread factor" of `color(green)m`

Given the vertex: `(color(red)2,color(blue)3)`
this becomes
`color(white)("XXX")color(brown)y=color(green)m(color(orange)x-color(red)2)^2+color(blue)3`

We are given that one solution point is `(color(orange)x,color(brown)y)=(color(orange)4,color(brown)11)`

So we have
`color(white)("XXX")color(brown)11=color(green)m(color(orange)4-color(red)2)^2+color(blue)3`

Simplifying:
`color(white)("XXX")8=color(green)m(2)^2`

`color(white)("XXX")8 =4color(green)m`

`color(white)("XXX")color(green)m=2`

We can substitute this back into our vertex equation, to get
`color(white)("XXX")color(brown)y=color(green)2(color(orange)x-color(red)2)^2+color(blue)3`

If your instructor prefers this in "standard form" we can expand the right side to get:
`color(white)("XXX")y=2x^2-8x+11`

For verification purposes, here is the graph of `y=2(x-2)^2+3`