Standard quadratic form is
#color(white)("XXX")y=ax^2+bx+c# for some constants #a,b,c#
#{:
("Given point:",color(white)("XXX"),"Implied equation:"),
((-1,-2),rArr,-2=a-b+c color(white)("XX")[1]),
((1,-4),rArr,-4=a+b+c color(white)("XX")[2]),
((2,1),rArr,1=4a+2b+c color(white)("XX")[3])
:}#
Subtracting [2] - [1]
#color(white)("XXX")-2=2bcolor(white)(*"XX")[4]#
#color(white)("XXX")rarrcolor(white)("XX")b=-1#
Substituting #(-1)# for #b# in [2] and [3]
#color(white)("XXX")-3=a+c color(white)("XX")[5]#
#color(white)("XXXx")3=4a+c color(white)("XX")[6]#
Subtracting [6]-[5]
#color(white)("XXX")6=3a#
#color(white)("XXX")rarr a=2#
Substituting #2# for #a# in [5]
#color(white)("XXX")-3=2+c#
#color(white)("XXX")rarr c=-5#
and the general quadratic standard equation: #y=ax^2+bx+c#
becomes
#color(white)("XXX")y=2x^2-1x-5#
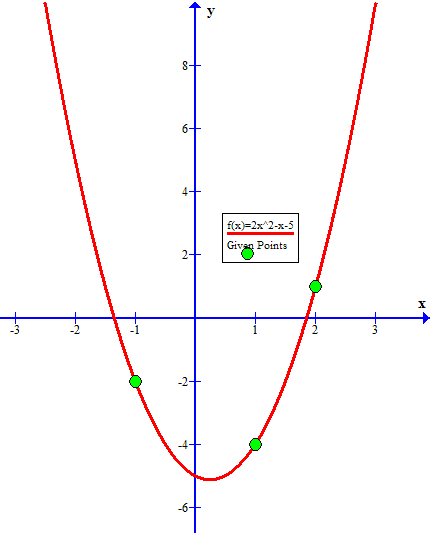
As a verification, here is the graph of #y=2x^2-x-5# and the given points: