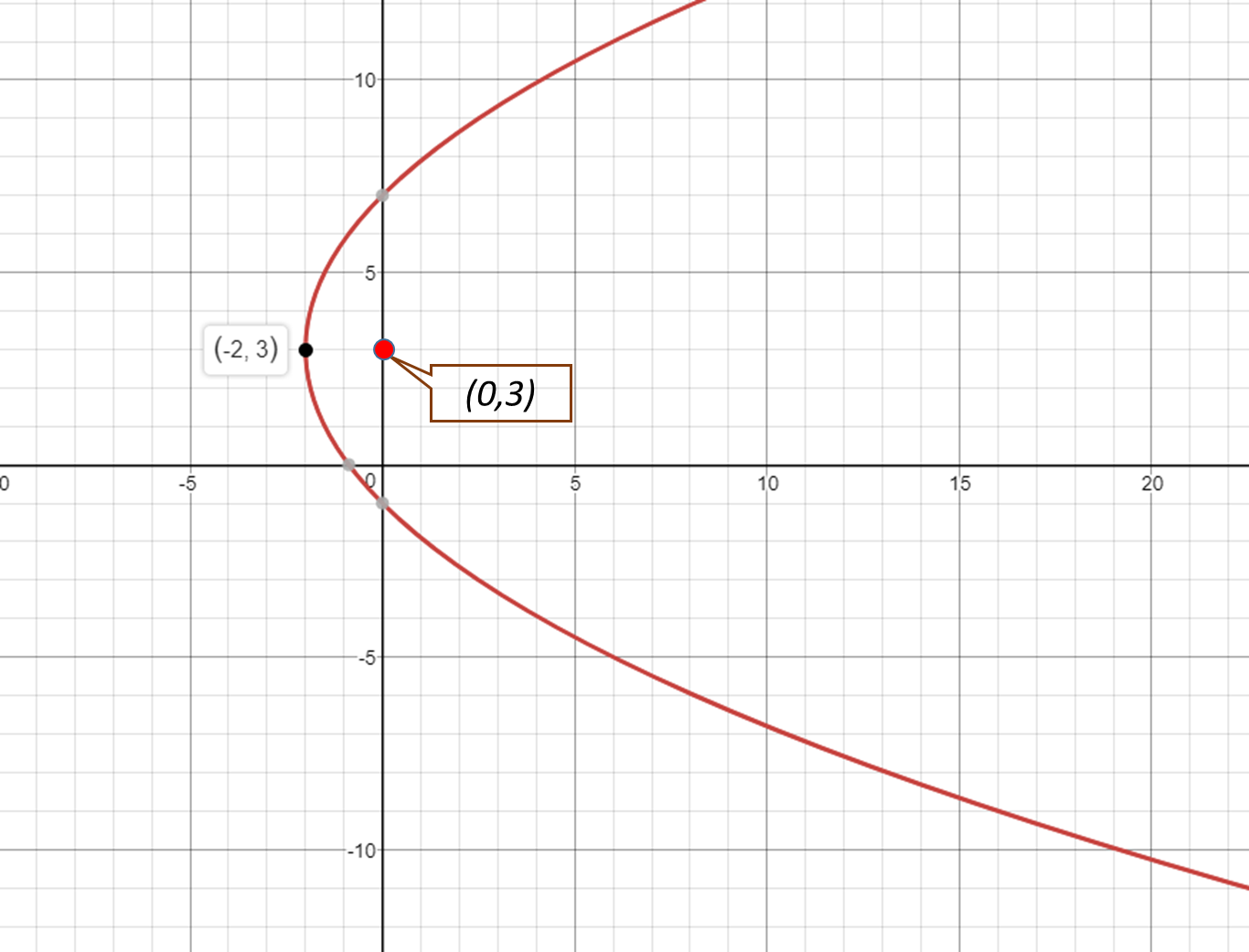
How do you write the equation of the parabola in vertex form given (-2,3) and focus (0,3)?

Question

4462 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-10T06:31:40

#(y-3)^2=8(x+2)#

Given -

Vertex #(-2, 3)#
Focus #(0, 3)#

The vertex is in the 2nd quadrant.
The focus is to the right of the vertex.
The parabola opens right.

The general form of such a parabola is

#(y-k)^2=4xxaxx(x-h)#

Where -

#k=3 -># y - coordinate of the vertex
#h=-2-># x - coordinate of the vertex
#a=2-># Distance between the vertex and the focus

Substitute these values in the given formula

#(y-3)^2=4xx 2xx(x-(-2))#

#(y-3)^2=8(x+2)#

enter image source here