Question

How do you write `y= (x-4)(x-2)` in standard form?

Answer 1

`y = x^2 - 6x + 8`

Explanation:

`y = (x-4)(x-2)`

The standard form of a quadratic equation is `ax^2 + bx + c`. To make this equation in standard form, we expand/simplify this using FOIL:

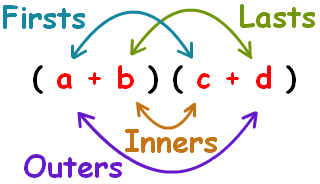
Following this image, we can multiply it out.

The `color(teal)("firsts")`:
`color(teal)(x*x) = x^2`

The `color(indigo)("outers")`:
`color(indigo)(x * -2) = -2x`

The `color(peru)"inners"`:
`color(peru)(-4 * x) = -4x`

The `color(olivedrab)"lasts"`:
`color(olivedrab)(-4 * -2) = 8`

Combine them all together to get:
`x^2 - 2x - 4x + 8`

We can still combine the like terms `color(blue)(-2x)` and `color(blue)(-4x)`:
`x^2 - 6x + 8`

As you can see, this matches the form `ax^2 + bx + c`. Therefore, the quadratic equation in standard form is `y = x^2-6x+8`.

Hope this helps!